文章目录

• • • • 文献参考
    • 基本概念
    • • 支持向量
      • 支持向量机(SVM)
      • 最大间隔超平面
      • 软间隔与硬间隔
    • SVM最优化问题求解思路
    • 支持向量机数学原理
    • • • 第一步：建立支持向量方程
        • 第二步：求出最大间隔LLL表达式
        • 第三步：求LLL约束条件，得出优化问题
        • 第四步：解出优化问题解的前四个条件
        • 第五步：得出优化问题解的第五个条件
        • 第六步：转化成SVM对偶问题
        • 第七步：优化方程
        • 第八步：得出算法步骤
  • 标题
  • • 升维转换与核技巧
    • 软间隔

文献参考

· 百度知道：桂纶美

基本概念

支持向量

概念：位于分类超平面附近的样本点，称为支持向量

在数学中，点这个概念常常用向量去取代。比如在直角坐标系下，点A坐标为(3,4)，我们可以认为它代表着向量OA = (3,4)

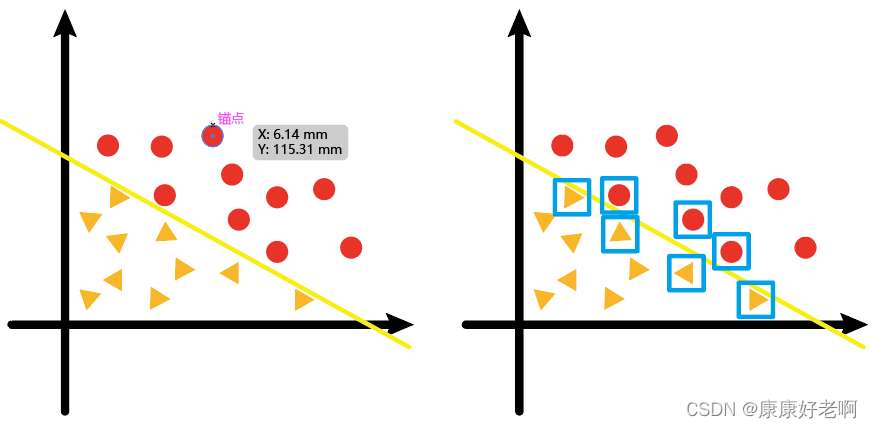
现在我们有如下左图的一个二维样本点（向量），其中黄色的线是经过线性回归计算得出来的分类线；而右图那些临近回归线的点（用蓝色方形标注），就叫做支持向量。

“支持” 的含义可以这样理解：

​ 那些临近分类边界的点，才是对回归线（超平面）的走向有影响的点；距离分类边界较远的点，它们对回归线（超平面）如何去画并没有什么影响

如果我们将“机”理解成“算法”，那么支持向量机不难理解为“与支持点相关的(求出分类超平面的)算法”

下面给出支持向量机较为标准的概念：

支持向量机(SVM)

是一种二分类模型，它的基本模型是定义在特征空间上的间隔最大的线性分类器。

对于下面这一些数据集，要用一条回归线将其分开，现有①、②、③三条线，哪一条效果最好呢？

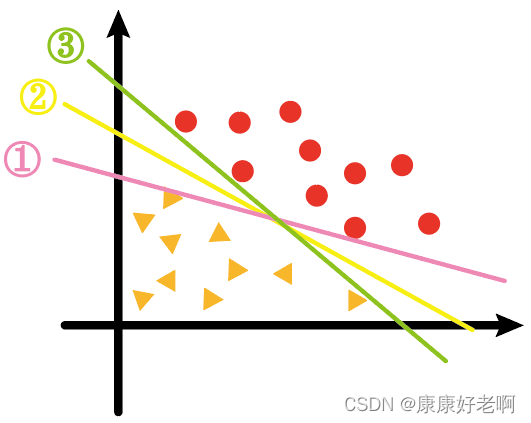
我想绝大部分人都会认为是②。虽然三条线都满足了将三角形和圆形分开，但是对于②线来说，三角形和圆形的支持向量到②线的距离看上去更加“均衡”，像是从中间位置将其分隔。

其实，支持向量机的意思是指：求支持向量到超平面的距离之和尽可能的大的算法。

事实上，根据基本不等式，距离之和最大和距离更加“均衡”其实是等价的

那么这里就引出了最大间隔超平面的概念

最大间隔超平面

上图中对应的②线——也就是我们看起来的最“均衡线”，它其实是以最大间隔把两类样本分开的线（高维的称作超平面），即最大间隔超平面。

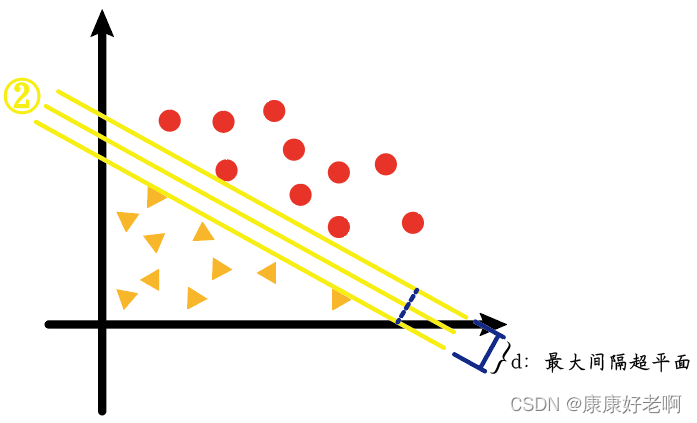
我们会发现①、③两条线的样本间隔要比②的小很多，如下图

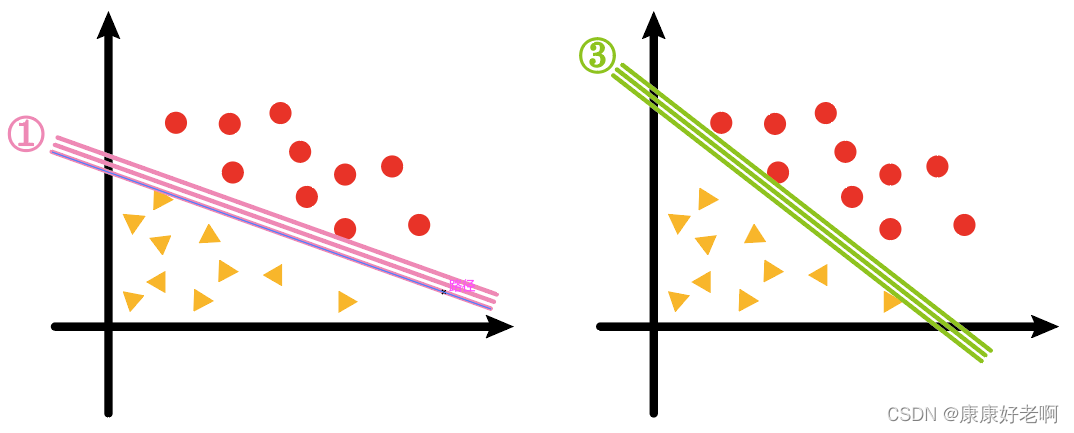
而我们支持向量机算法（SVM）实质上求的就是②这样的线、平面或者超平面

软间隔与硬间隔

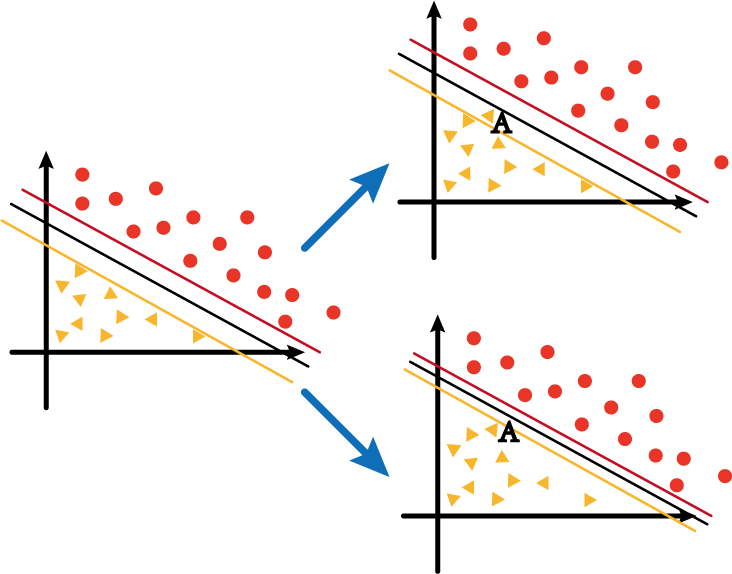
假设上图中左边的坐标系中黄色、黑色和红色分别为负/决策/正超平面，而此时如果在黄线和红线之间新增了一个数据点AAA，那么围绕超平面是否进行调整，会分成两种情况：

• 第一种就是右上角的图1，虽然加入了AAA，但是仍然使其在黄线与红线之间；
• 第二种就是右下角的图2，随着AAA的加入，超平面也随之发生变化，最终保证AAA在黄线之下。

第一种情况中的黄线与红线的距离我们称之为软间隔；第二种情况中的黄线与红线的距离我们称之为硬间隔。

SVM最优化问题求解思路

在线性代数中，任意超平面可以用下面这个线性方程来描述：
WTX+b=0W^{T}X+b=0 WTX+b=0
其中
W=[w1,w2,⋅⋅⋅，wn]W=[w_1,w_2,···，w_n] W=[w1​,w2​,⋅⋅⋅，wn​]

X=[x1,x2,⋅⋅⋅，xn]X=[x_1,x_2,···，x_n] X=[x1​,x2​,⋅⋅⋅，xn​]

为系数矩阵，矩阵W转置后

[W1W2⋅⋅⋅Wn]\left[ \begin{array} {} W_1\\ W_2\\ ·\\ ·\\ ·\\ W_n \end{array} \right] ​W1​W2​⋅⋅⋅Wn​​​

$$

故
WTX=w1x1+w2x2+w3x3+⋅⋅⋅+wnxnW^TX=w_1x_1+w_2x_2+w_3x_3+···+w_nx_n WTX=w1​x1​+w2​x2​+w3​x3​+⋅⋅⋅+wn​xn​
就是我们正常看到的超平面函数表达式

根据点到直线的距离公式

∣Ax+By+C∣A2+B2\frac{|Ax+By+C|}{\sqrt{A^2+B^2}} A2+B2​∣Ax+By+C∣​
从二维拓展成高维
∣w1x1+w2x2+w3x3+⋅⋅⋅+wnxn+b∣w12+w22+⋅⋅⋅+wn2\frac{|w_1x_1+w_2x_2+w_3x_3+···+w_nx_n+b|}{\sqrt{w_1^2+w_2^2+···+w_n^2}} w12​+w22​+⋅⋅⋅+wn2​​∣w1​x1​+w2​x2​+w3​x3​+⋅⋅⋅+wn​xn​+b∣​
其中
w1x1+w2x2+w3x3+⋅⋅⋅+wnxn=WTXw_1x_1+w_2x_2+w_3x_3+···+w_nx_n=W^TX w1​x1​+w2​x2​+w3​x3​+⋅⋅⋅+wn​xn​=WTX
为前面所得出的公式
w12+w22+⋅⋅⋅+wn2=∣∣W∣∣\sqrt{w_1^2+w_2^2+···+w_n^2}=||W|| w12​+w22​+⋅⋅⋅+wn2​​=∣∣W∣∣
为向量的模的定义

对于二维向量 X = (3,4)，其模
∣∣X∣∣=32+42=5||X||=\sqrt{3^2+4^2}=5 ∣∣X∣∣=32+42​=5
高维向量以此类推

所以上面的高维距离公式可以转化为

∣WTX+b∣∣∣W∣∣\frac{|W^TX+b|}{||W||} ∣∣W∣∣∣WTX+b∣​

支持向量机数学原理

通过上文介绍，我们大概了解了支持向量机的作用与简单原理。下面我们详细介绍一下支持向量机的数学原理以及其算法。

• 第一步：建立支持向量方程

首先补充一下上文介绍超平面的内容。我们一般将中间的用于分隔的超平面叫做决策超平面，决策超平面也是我们最后求得的超平面。而决策超平面的正方向与负方向分别有两个超平面：正超平面和负超平面。这两个超平面用于辅助生成决策超平面。为了简单化，我们先只考虑二维的支持向量机。

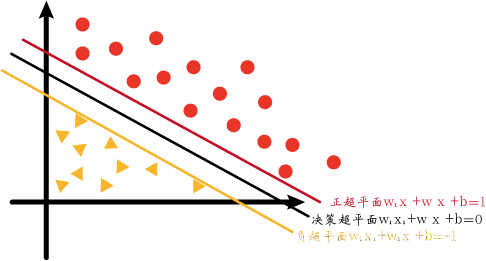
图中正超平面、决策超平面、负超平面的方程分别如下：
w1x1+w2x2+b=1w1x1+w2x2+b=0w1x1+w2x2+b=−1w_1x_1+w_2x_2+b=1\\w_1x_1+w_2x_2+b=0\\w_1x_1+w_2x_2+b=-1 w1​x1​+w2​x2​+b=1w1​x1​+w2​x2​+b=0w1​x1​+w2​x2​+b=−1
这个并非是超平面的唯一写法。前面基础部分我们介绍了线性方程如何用矩阵来表达，这种写法只是上面的一种等价变式（移项），方便后面的运算。

现在我们假设在正超平面和负超平面上分别有两个支持向量M和N。他们分别满足下式：
w1x1m+w2x2m+b=1w1x1n+w2x2n+b=−1w_1x_{1m}+w_2x_{2m}+b=1\\w_1x_{1n}+w_2x_{2n}+b=-1 w1​x1m​+w2​x2m​+b=1w1​x1n​+w2​x2n​+b=−1
目前现有的这两个方程对我们并没有什么作用或者启发，考虑到两个式子中都可以提出公因子w1、w2w_1、w_2w1​、w2​，以及都有常数bbb，所以我们将两式作差，会得到如下结果：
w1(x1m−x1n)+w2(x2m−x2n)=2w_1(x_{1m}-x_{1n})+w_2(x_{2m}-x_{2n})=2 w1​(x1m​−x1n​)+w2​(x2m​−x2n​)=2
如果我们将上述式子看成两个向量做点积，我们会得到：
w⃗(xm⃗−xn⃗)=2\vec{w}(\vec{x_m}-\vec{x_n})=2 w(xm​​−xn​​)=2
其中w⃗=[w1w2]\vec{w}=[w_1 \ w_2]w=[w1​ w2​]，xm⃗=[x1mx2m]T\vec{x_m}=[x_{1m} \ x_{2m}]^Txm​​=[x1m​ x2m​]T，xn⃗=[x1nx2n]T\vec{x_n}=[x_{1n} \ x_{2n}]^Txn​​=[x1n​ x2n​]T

根据a⃗⋅b⃗=∣∣a⃗∣∣∗∣∣b⃗∣∣∗cosθ\vec{a}·\vec{b}=||\vec{a}||*||\vec{b}||*cos\thetaa⋅b=∣∣a∣∣∗∣∣b∣∣∗cosθ，
∣∣w⃗∣∣∗∣∣xm⃗−xn⃗∣∣∗cosθ=2||\vec{w}||*||\vec{x_m}-\vec{x_n}||*cos\theta=2 ∣∣w∣∣∗∣∣xm​​−xn​​∣∣∗cosθ=2
其中∣∣w⃗∣∣=w12+w22||\vec{w}||=\sqrt{w_1^2+w_2^2}∣∣w∣∣=w12​+w22​​。

移项
∣∣xm⃗−xn⃗∣∣∗cosθ=2∣∣w⃗∣∣||\vec{x_m}-\vec{x_n}||*cos\theta=\frac{2}{||\vec{w}||} ∣∣xm​​−xn​​∣∣∗cosθ=∣∣w∣∣2​

通过移项xxx与www分别在等式左右两边。左边是数据点的坐标，右边是待求的权重值。

• 第二步：求出最大间隔LLL表达式

这里我们不妨思考下 ∣∣xm⃗−xn⃗∣∣∗cosθ||\vec{x_m}-\vec{x_n}||*cos\theta∣∣xm​​−xn​​∣∣∗cosθ 的意义。

所以我们画出下图，尝试从几何角度去观察上式的意义。

我们知道向量点积可以转化为投影，即将一个向量的模乘cosθcos\thetacosθ投影到另外一个向量的方向上，相同方向会极大的方便计算。

于是我们画出了下面的坐标系与向量（称为图1）。我们想用向量点积投影，但是我们并不知道MN和w⃗\vec{w}w的夹角。

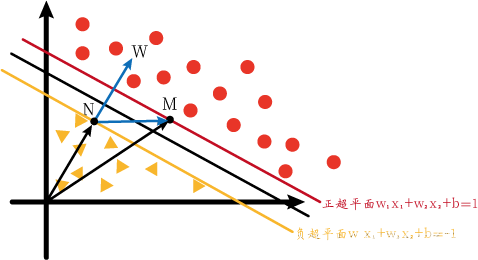
但是我们可以进行转化。我们知道M、N两点在正负超平面上，那如果M、N在决策超平面上呢？由于这三个超平面的方程只有等号右边的常数不一样，所以如果M、N在决策超平面上时的w⃗\vec{w}w应该与上图的一样。所以我们不妨先设M、N在决策超平面上。我们可以画出下图（称为图2）：

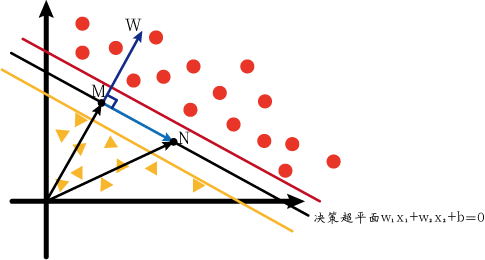
此时的M、N分别满足下列式子：
w1x1m+w2x2m+b=0w1x1n+w2x2n+b=0w_1x_{1m}+w_2x_{2m}+b=0\\w_1x_{1n}+w_2x_{2n}+b=0 w1​x1m​+w2​x2m​+b=0w1​x1n​+w2​x2n​+b=0
两式作差，可以得到：
w1(x1m−x1n)+w2(x2m−x2n)=0w_1(x_{1m}-x_{1n})+w_2(x_{2m}-x_{2n})=0 w1​(x1m​−x1n​)+w2​(x2m​−x2n​)=0
即
w⃗(xm⃗−xn⃗)=0\vec{w}(\vec{x_m}-\vec{x_n})=0 w(xm​​−xn​​)=0
向量点积为零说明两向量互相垂直。观察上图，xm⃗−xn⃗\vec{x_m}-\vec{x_n}xm​​−xn​​即为NM⃗\vec{NM}NM。而这也就意味着w⃗\vec{w}w垂直于决策超平面，也就垂直与正、负超平面。好，这时我们从图2转回图1，我们再次将图1放出来方便说明。

由于w⃗\vec{w}w垂直于超平面，所以∣∣NM⃗∣∣||\vec{NM}||∣∣NM∣∣在w⃗\vec{w}w上的投影就为正负超平面的最大间隔LLL。而正好∣∣NM⃗∣∣=∣∣xm⃗−xn⃗∣∣∗cosθ||\vec{NM}||=||\vec{x_m}-\vec{x_n}||*cos\theta∣∣NM∣∣=∣∣xm​​−xn​​∣∣∗cosθ，故
L=2∣∣w⃗∣∣L=\frac{2}{||\vec{w}||} L=∣∣w∣∣2​

• 第三步：求LLL约束条件，得出优化问题

正超平面：所有红点属于正类，所以yi=1y_i=1yi​=1；所有红点都在正超平面上方，所以w⃗⋅xi⃗+b≥1\vec{w}·\vec{x_i}+b≥1w⋅xi​​+b≥1

负超平面：所有黄点属于负类，所以yi=−1y_i=-1yi​=−1；所有黄点都在负超平面下方，所以w⃗⋅xi⃗+b≤1\vec{w}·\vec{x_i}+b≤1w⋅xi​​+b≤1

上面两种情况可以总结成下面这个式子：
yi∗(w⃗⋅xi⃗+b)≥1y_i*(\vec{w}·\vec{x_i}+b)≥1 yi​∗(w⋅xi​​+b)≥1
而这个式子就是约束条件。

所以，求决策超平面问题就转化为：

在yi∗(w⃗⋅xi⃗+b)≥1y_i*(\vec{w}·\vec{x_i}+b)≥1yi​∗(w⋅xi​​+b)≥1条件下，∣∣w⃗∣∣||\vec{w}||∣∣w∣∣的最小值。

由于∣∣w⃗∣∣=w12+w22||\vec{w}||=\sqrt{w_1^2+w_2^2}∣∣w∣∣=w12​+w22​​中含有根号，所以最小值并不是很好求。所以我们转化一下，将∣∣w⃗∣∣||\vec{w}||∣∣w∣∣转化成∣∣w⃗∣∣22\frac{||\vec{w}||^2}{2}2∣∣w∣∣2​，于是问题等价为：

在yi∗(w⃗⋅xi⃗+b)≥1y_i*(\vec{w}·\vec{x_i}+b)≥1yi​∗(w⋅xi​​+b)≥1条件下，∣∣w⃗∣∣22\frac{||\vec{w}||^2}{2}2∣∣w∣∣2​的最小值。

• 第四步：解出优化问题解的前四个条件

这种问题我们会通过拉格朗日乘子法进行求解。

但是有一个问题，就是约束条件yi∗(w⃗⋅xi⃗+b)≥1y_i*(\vec{w}·\vec{x_i}+b)≥1yi​∗(w⋅xi​​+b)≥1是不等式而不是等式，所以我们要先经过一步转化，将不等式转化为等式。

我们将yi∗(w⃗⋅xi⃗+b)≥1y_i*(\vec{w}·\vec{x_i}+b)≥1yi​∗(w⋅xi​​+b)≥1转换成yi∗(w⃗⋅xi⃗+b)−1=pi2y_i*(\vec{w}·\vec{x_i}+b)-1=p_i^2yi​∗(w⋅xi​​+b)−1=pi2​，由于pi2≥0p_i^2≥0pi2​≥0恒成立，故yi∗(w⃗⋅xi⃗+b)−1≥0y_i*(\vec{w}·\vec{x_i}+b)-1≥0yi​∗(w⋅xi​​+b)−1≥0恒成立。

所以原问题等价为：

在yi∗(w⃗⋅xi⃗+b)−1=pi2y_i*(\vec{w}·\vec{x_i}+b)-1=p_i^2yi​∗(w⋅xi​​+b)−1=pi2​条件下，∣∣w⃗∣∣22\frac{||\vec{w}||^2}{2}2∣∣w∣∣2​的最小值。

下面构造拉格朗日函数：
L(w,b,λi,pi)=∣∣w⃗∣∣22−∑i=1sλi∗(yi∗(w⃗⋅xi⃗+b)−1−pi2)L(w,b,\lambda_i,p_i)=\frac{||\vec{w}||^2}{2}-\sum_{i=1}^s\lambda_i*(y_i*(\vec{w}·\vec{x_i}+b)-1-p_i^2) L(w,b,λi​,pi​)=2∣∣w∣∣2​−i=1∑s​λi​∗(yi​∗(w⋅xi​​+b)−1−pi2​)
然后进行求解。拉格朗日函数对每个未知数求偏导并令其等于0。
∂L∂w=0;∂L∂b=0;∂L∂λi=0;∂L∂pi=0\frac{\partial{L}}{\partial{w}}=0;\frac{\partial{L}}{\partial{b}}=0;\frac{\partial{L}}{\partial{\lambda_i}}=0;\frac{\partial{L}}{\partial{p_i}}=0 ∂w∂L​=0;∂b∂L​=0;∂λi​∂L​=0;∂pi​∂L​=0
下面我们一个个来计算。

• 首先是∂L∂w=0\frac{\partial{L}}{\partial{w}}=0∂w∂L​=0。www出现在两个位置，分别是∣∣w⃗∣∣22\frac{||\vec{w}||^2}{2}2∣∣w∣∣2​和∑i=1sλi∗yi∗(w⃗⋅xi⃗+b)\sum_{i=1}^s\lambda_i*y_i*(\vec{w}·\vec{x_i}+b)∑i=1s​λi​∗yi​∗(w⋅xi​​+b)，很容易求导得下式：

w⃗−∑i=1sλiyixi⃗=0⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅①\vec{w}-\sum_{i=1}^s\lambda_iy_i\vec{x_i}=0············① w−i=1∑s​λi​yi​xi​​=0⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅①

• 然后是∂L∂b=0\frac{\partial{L}}{\partial{b}}=0∂b∂L​=0。bbb只出现在一个位置，为∑i=1sλi∗yi∗b\sum_{i=1}^s\lambda_i*y_i*b∑i=1s​λi​∗yi​∗b，很容易求导得下式：

∑i=1sλiyi=0⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅②\sum_{i=1}^s\lambda_iy_i=0············② i=1∑s​λi​yi​=0⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅②

• 接着是∂L∂λi=0\frac{\partial{L}}{\partial{\lambda_i}}=0∂λi​∂L​=0。λi\lambda_iλi​只出现在一个位置，为∑i=1sλi∗(yi∗(w⃗⋅xi⃗+b)−1−pi2)\sum_{i=1}^s\lambda_i*(y_i*(\vec{w}·\vec{x_i}+b)-1-p_i^2)∑i=1s​λi​∗(yi​∗(w⋅xi​​+b)−1−pi2​)。本来求偏导得到的结果应该是∑i=1syi∗(w⃗⋅xi⃗+b)−1−pi2=0\sum_{i=1}^{s}{y_i*(\vec{w}·\vec{x_i}+b)-1-p_i^2=0}∑i=1s​yi​∗(w⋅xi​​+b)−1−pi2​=0，但其实根据限制条件，yi∗(w⃗⋅xi⃗+b)−1−pi2=0y_i*(\vec{w}·\vec{x_i}+b)-1-p_i^2=0yi​∗(w⋅xi​​+b)−1−pi2​=0，没有必要使用求和符号。

yi∗(w⃗⋅xi⃗+b)−1−pi2=0⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅③y_i*(\vec{w}·\vec{x_i}+b)-1-p_i^2=0············③ yi​∗(w⋅xi​​+b)−1−pi2​=0⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅③

• 最后是∂L∂pi=0\frac{\partial{L}}{\partial{p_i}}=0∂pi​∂L​=0。pip_ipi​只出现在一个位置，为∑i=1sλi∗(−pi2)\sum_{i=1}^s\lambda_i*(-p_i^2)∑i=1s​λi​∗(−pi2​)，很容易求导得到下式：

2λipi=0⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅④2\lambda_ip_i=0············④ 2λi​pi​=0⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅④

下面的步骤就是利用①~④式和原式求出∣∣w⃗∣∣||\vec{w}||∣∣w∣∣的最小值。首先我们将④式左右两边同时除以2并乘pip_ipi​，得到下式：
λipi2=0\lambda_ip_i^2=0 λi​pi2​=0
之所以要这样做是因为③式中有一个pi2p_i^2pi2​，这样做可以一定程度上化简计算。我们将③式代入④式，得到：
λi(yi∗(w⃗⋅xi⃗+b)−1)=0\lambda_i(y_i*(\vec{w}·\vec{x_i}+b)-1)=0 λi​(yi​∗(w⋅xi​​+b)−1)=0
这个式子非常有趣。之前我们在第三步得到yi∗(w⃗⋅xi⃗+b)≥1y_i*(\vec{w}·\vec{x_i}+b)≥1yi​∗(w⋅xi​​+b)≥1这个约束条件，那这样上式只可能在两种情况下成立：

① yi∗(w⃗⋅xi⃗+b)−1)＞0y_i*(\vec{w}·\vec{x_i}+b)-1)＞0yi​∗(w⋅xi​​+b)−1)＞0，λi=0\lambda_i=0λi​=0;

② yi∗(w⃗⋅xi⃗+b)−1=0y_i*(\vec{w}·\vec{x_i}+b)-1=0yi​∗(w⋅xi​​+b)−1=0，λi≠0\lambda_i≠0λi​=0。

• 第五步：得出优化问题解的第五个条件

对于拉格朗日函数L(w,b,λi,pi)=∣∣w⃗∣∣22−∑i=1sλi∗(yi∗(w⃗⋅xi⃗+b)−1−pi2)L(w,b,\lambda_i,p_i)=\frac{||\vec{w}||^2}{2}-\sum_{i=1}^s\lambda_i*(y_i*(\vec{w}·\vec{x_i}+b)-1-p_i^2)L(w,b,λi​,pi​)=2∣∣w∣∣2​−∑i=1s​λi​∗(yi​∗(w⋅xi​​+b)−1−pi2​)来说，当不满足约束条件时，即yi∗(w⃗⋅xi⃗+b)−1<0y_i*(\vec{w}·\vec{x_i}+b)-1<0yi​∗(w⋅xi​​+b)−1<0时，如果λi<0\lambda_i<0λi​<0，则∑i=1sλi∗(yi∗(w⃗⋅xi⃗+b)−1−pi2)>0\sum_{i=1}^s\lambda_i*(y_i*(\vec{w}·\vec{x_i}+b)-1-p_i^2)>0∑i=1s​λi​∗(yi​∗(w⋅xi​​+b)−1−pi2​)>0，而L(w,b,λi,pi)L(w,b,\lambda_i,p_i)L(w,b,λi​,pi​)也会更小。根据拉格朗日函数的性质，越符合约束条件拉格朗日函数的值越小。这就说明，λi\lambda_iλi​小于0是不符合常理的，故其应该大于等于0。

我们同样也可以通过图像来解释这个问题。

我们假设是二维空间，在这个二维空间中，横纵坐标分别是w1w_1w1​和w2w_2w2​，那么∣∣w⃗∣∣=w12+w22||\vec{w}||=\sqrt{w_1^2+w_2^2}∣∣w∣∣=w12​+w22​​在图像上表示的几何含义为一个圆心为原点，半径为w12+w22\sqrt{w_1^2+w_2^2}w12​+w22​​的圆。

我们所要求得的优化问题min∣∣w⃗∣∣22min\frac{||\vec{w}||^2}{2}min2∣∣w∣∣2​，即为∣∣w⃗∣∣||\vec{w}||∣∣w∣∣取最小值时取到。而由于∣∣w⃗∣∣||\vec{w}||∣∣w∣∣即为圆的半径，所以我们希望圆尽可能的小。

现在我们加入约束条件。第一个约束条件为g1=y1∗(w⃗⋅x1⃗+b)−1≥0g_1=y_1*(\vec{w}·\vec{x_1}+b)-1≥0g1​=y1​∗(w⋅x1​​+b)−1≥0，它在图像上表示的含义是可行区域在一条直线之上（浅绿色），如下图：

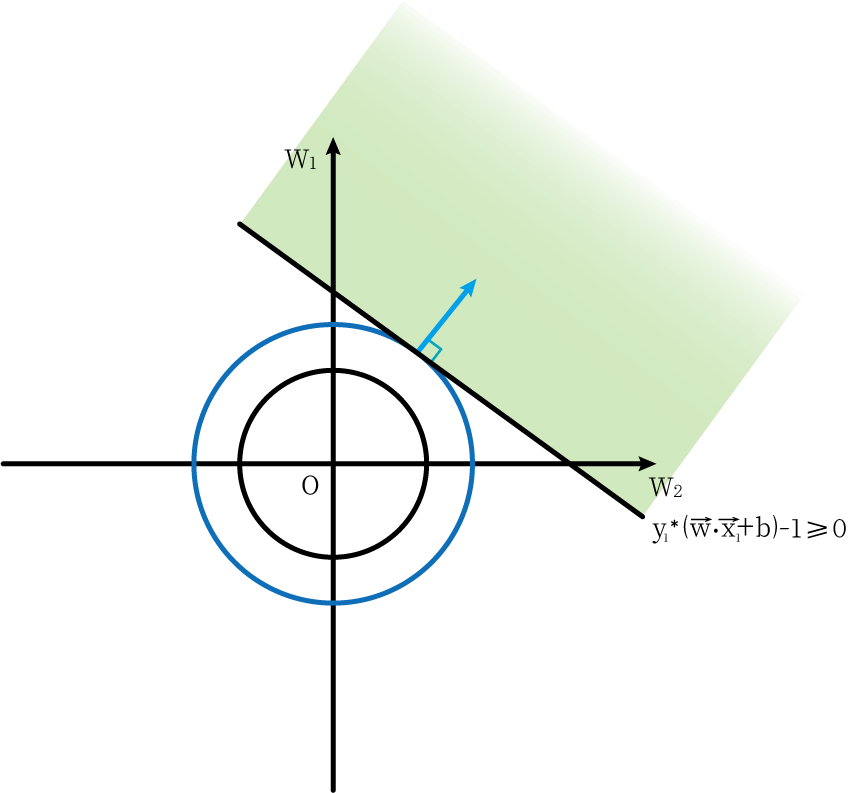
而能够使圆上有点能在可行区域之内，且圆的半径要最小的情况就是圆与直线相切（如图中深蓝色圆所表示）

此时我们加入另外一个限制条件，g2=y2∗(w⃗⋅x2⃗+b)−1≥0g_2=y_2*(\vec{w}·\vec{x_2}+b)-1≥0g2​=y2​∗(w⋅x2​​+b)−1≥0。此时在两个限制条件下，最小的圆是经过两条直线交点的圆。而此时的w⃗=(w1,w2)\vec{w}=(w_1,w_2)w=(w1​,w2​)的方向（红色线所表示）只要在两个直线之内即可。

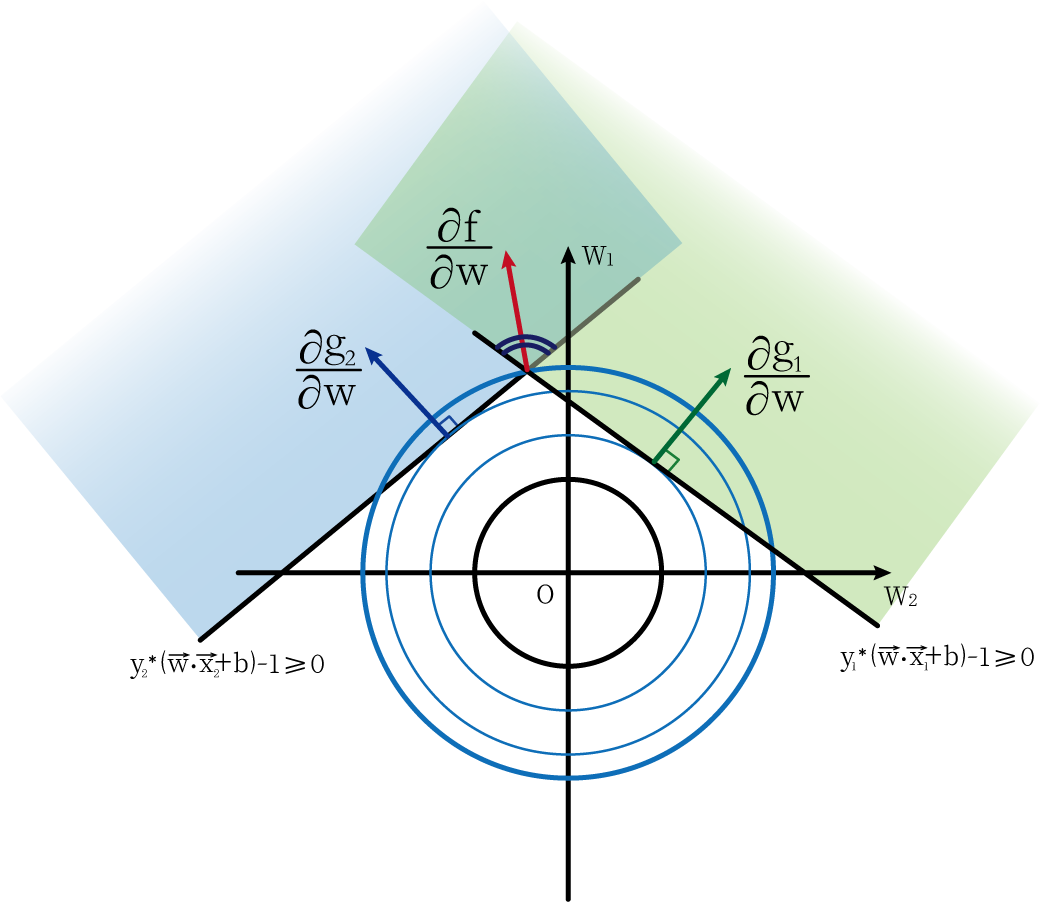
通过上图直观理解，我们也可以得出下面一个式子：向量∂f∂w\frac{\partial{f}}{\partial{w}}∂w∂f​可以由∂g1∂w和∂g2∂w\frac{\partial{g_1}}{\partial{w}}和\frac{\partial{g_2}}{\partial{w}}∂w∂g1​​和∂w∂g2​​线性表出，而它们的系数λ1\lambda_1λ1​和λ2\lambda_2λ2​都为非负数（通过直观理解或者用矢量三角形理解）。
∂f∂w=λ1∂g1∂w+λ2∂g2∂w\frac{\partial{f}}{\partial{w}}=\lambda_1\frac{\partial{g_1}}{\partial{w}}+\lambda_2\frac{\partial{g_2}}{\partial{w}} ∂w∂f​=λ1​∂w∂g1​​+λ2​∂w∂g2​​
通过上述图像也可以帮助我们理解，λi\lambda_iλi​为什么大于等于0。我们也就得到了第五个条件：
λi≥0⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⑤\lambda_i≥0············⑤ λi​≥0⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⑤
综合上述，我们已经得到了解的五个条件，又称为KKT条件：
w⃗−∑i=1sλiyixi⃗=0⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅①∑i=1sλiyi=0⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅②yi∗(w⃗⋅xi⃗+b)−1−pi2=0⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅③2λipi=0⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅④λi≥0⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⑤\vec{w}-\sum_{i=1}^s\lambda_iy_i\vec{x_i}=0····················①\\\sum_{i=1}^s\lambda_iy_i=0·························②\\y_i*(\vec{w}·\vec{x_i}+b)-1-p_i^2=0············③\\2\lambda_ip_i=0····························④\\\lambda_i≥0·······························⑤ w−i=1∑s​λi​yi​xi​​=0⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅①i=1∑s​λi​yi​=0⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅②yi​∗(w⋅xi​​+b)−1−pi2​=0⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅③2λi​pi​=0⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅④λi​≥0⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⑤

• 第六步：转化成SVM对偶问题

对偶问题是一种求解线性规划问题的常用方法。通过将一个问题转化为其对偶问题，有时能大大简化求解问题的难度。

我们先回顾一下原问题：

在gi(w,b)=yi∗(w⃗⋅xi⃗+b)−1=pi2g_i(w,b)=y_i*(\vec{w}·\vec{x_i}+b)-1=p_i^2gi​(w,b)=yi​∗(w⋅xi​​+b)−1=pi2​条件下，求∣∣w⃗∣∣22求\frac{||\vec{w}||^2}{2}求2∣∣w∣∣2​的最小值。

我们先假设原问题的最优解为w∗、b∗w^*、b^*w∗、b∗。然后设
q(λi)=min(L(w,b,λi))=min(∣∣w⃗∣∣22−∑i=1sλi∗(yi∗(w⃗⋅xi⃗+b)−1−pi2))q(\lambda_i)=min(L(w,b,\lambda_i))=min(\frac{||\vec{w}||^2}{2}-\sum_{i=1}^s\lambda_i*(y_i*(\vec{w}·\vec{x_i}+b)-1-p_i^2)) q(λi​)=min(L(w,b,λi​))=min(2∣∣w∣∣2​−i=1∑s​λi​∗(yi​∗(w⋅xi​​+b)−1−pi2​))
代入w∗、b∗w^*、b^*w∗、b∗，可以得到下面的式子：
q(λi)=min(L(w,b,λi))≤min(L(w∗,b∗,λi))q(\lambda_i)=min(L(w,b,\lambda_i))≤min(L(w^*,b^*,\lambda_i)) q(λi​)=min(L(w,b,λi​))≤min(L(w∗,b∗,λi​))
即 min(∣∣w⃗∣∣22−∑i=1sλi∗(yi∗(w⃗⋅xi⃗+b)−1−pi2))≤∣∣w∗⃗∣∣22−∑i=1sλi∗(yi∗(w∗⃗⋅xi⃗+b∗)−1−pi2)min(\frac{||\vec{w}||^2}{2}-\sum_{i=1}^s\lambda_i*(y_i*(\vec{w}·\vec{x_i}+b)-1-p_i^2))≤\frac{||\vec{w^*}||^2}{2}-\sum_{i=1}^s\lambda_i*(y_i*(\vec{w^*}·\vec{x_i}+b^*)-1-p_i^2)min(2∣∣w∣∣2​−∑i=1s​λi​∗(yi​∗(w⋅xi​​+b)−1−pi2​))≤2∣∣w∗∣∣2​−∑i=1s​λi​∗(yi​∗(w∗⋅xi​​+b∗)−1−pi2​)

小于等于号的存在是由minminmin最小值函数决定的。

根据KKT条件的③和⑤，∑i=1sλi∗(yi∗(w∗⃗⋅xi⃗+b∗)−1−pi2)\sum_{i=1}^s\lambda_i*(y_i*(\vec{w^*}·\vec{x_i}+b^*)-1-p_i^2)∑i=1s​λi​∗(yi​∗(w∗⋅xi​​+b∗)−1−pi2​)必定大于0，故
∣∣w∗⃗∣∣22−∑i=1sλi∗(yi∗(w∗⃗⋅xi⃗+b∗)−1−pi2)≤∣∣w∗⃗∣∣22\frac{||\vec{w^*}||^2}{2}-\sum_{i=1}^s\lambda_i*(y_i*(\vec{w^*}·\vec{x_i}+b^*)-1-p_i^2)≤\frac{||\vec{w^*}||^2}{2} 2∣∣w∗∣∣2​−i=1∑s​λi​∗(yi​∗(w∗⋅xi​​+b∗)−1−pi2​)≤2∣∣w∗∣∣2​
又由于w∗⃗\vec{w^*}w∗是原问题最优解，所以我们可以得到：
∣∣w∗⃗∣∣22≤∣∣w⃗∣∣22\frac{||\vec{w^*}||^2}{2}≤\frac{||\vec{w}||^2}{2} 2∣∣w∗∣∣2​≤2∣∣w∣∣2​
所以我们可以得到下面一个不等式链：
q(λi)≤min(L(w∗,b∗,λi))≤∣∣w∗⃗∣∣22≤∣∣w⃗∣∣22q(\lambda_i)≤min(L(w^*,b^*,\lambda_i))≤\frac{||\vec{w^*}||^2}{2}≤\frac{||\vec{w}||^2}{2} q(λi​)≤min(L(w∗,b∗,λi​))≤2∣∣w∗∣∣2​≤2∣∣w∣∣2​
我们假设λi∗为q(λi)\lambda_i^*为q(\lambda_i)λi∗​为q(λi​)的最优解。则
q(λi)≤q(λi∗)≤∣∣w∗⃗∣∣22≤∣∣w⃗∣∣22q(\lambda_i)≤q(\lambda_i^*)≤\frac{||\vec{w^*}||^2}{2}≤\frac{||\vec{w}||^2}{2} q(λi​)≤q(λi∗​)≤2∣∣w∗∣∣2​≤2∣∣w∣∣2​
好，进行到这一步我们就可以将原问题转化成对偶问题了。

原问题：

• 在gi(w,b)=yi∗(w⃗⋅xi⃗+b)−1≥0g_i(w,b)=y_i*(\vec{w}·\vec{x_i}+b)-1≥0gi​(w,b)=yi​∗(w⋅xi​​+b)−1≥0条件下，求∣∣w⃗∣∣22求\frac{||\vec{w}||^2}{2}求2∣∣w∣∣2​的最小值。

对偶问题：

• 在λi≥0\lambda_i≥0λi​≥0的条件下，求q(λi)=min(L(w,b,λi))q(\lambda_i)=min(L(w,b,\lambda_i))q(λi​)=min(L(w,b,λi​))的最大值。

当q(λi∗)=∣∣w∗⃗∣∣22q(\lambda_i^*)=\frac{||\vec{w^*}||^2}{2}q(λi∗​)=2∣∣w∗∣∣2​时，两个问题为强对偶问题，应同时取得最优解，下面进行证明：

因为
q(λi)≤∣∣w⃗∣∣22q(\lambda_i)≤\frac{||\vec{w}||^2}{2} q(λi​)≤2∣∣w∣∣2​
所以
q(λi∗)≤∣∣w⃗∣∣22q(\lambda_i^*)≤\frac{||\vec{w}||^2}{2} q(λi∗​)≤2∣∣w∣∣2​
故
∣∣w∗⃗∣∣22≤∣∣w⃗∣∣22\frac{||\vec{w^*}||^2}{2}≤\frac{||\vec{w}||^2}{2} 2∣∣w∗∣∣2​≤2∣∣w∣∣2​
而又根据前面得到的q(λi)≤min(L(w∗,b∗,λi))≤∣∣w∗⃗∣∣22q(\lambda_i)≤min(L(w^*,b^*,\lambda_i))≤\frac{||\vec{w^*}||^2}{2}q(λi​)≤min(L(w∗,b∗,λi​))≤2∣∣w∗∣∣2​，所以
q(λi)≤∣∣w∗⃗∣∣22=q(λi∗)q(\lambda_i)≤\frac{||\vec{w^*}||^2}{2}=q(\lambda_i^*) q(λi​)≤2∣∣w∗∣∣2​=q(λi∗​)
所以q(λi∗)q(\lambda_i^*)q(λi∗​)为q(λi)q(\lambda_i)q(λi​)的最大值解。

故证明在强对偶条件下，原问题和对偶问题的最优解同时取到。

• 第七步：优化方程

根据前面的拉格朗日函数，我们已经得到：
max(q(λ))=max(min(∣∣w⃗∣∣2)−∑i=1sλi∗(yi∗(w∗⃗⋅xi⃗+b∗)−1)))max(q(\lambda))=max(min(\frac{||\vec{w}||}{2})-\sum_{i=1}^s\lambda_i*(y_i*(\vec{w^*}·\vec{x_i}+b^*)-1))) max(q(λ))=max(min(2∣∣w∣∣​)−i=1∑s​λi​∗(yi​∗(w∗⋅xi​​+b∗)−1)))
将KKT条件代入化简可得：
max(q(λ))=max(∑i=1sλi−12∑i=1s∑j=1sλiλjyiyjxi⃗⋅xj⃗)max(q(\lambda))=max(\sum_{i=1}^s{\lambda_i}-\frac{1}{2}\sum_{i=1}^{s}\sum_{j=1}^s\lambda_i\lambda_jy_iy_j\vec{x_i}·\vec{x_j}) max(q(λ))=max(i=1∑s​λi​−21​i=1∑s​j=1∑s​λi​λj​yi​yj​xi​​⋅xj​​)

• 第八步：得出算法步骤

上文我们推导过下列式子：

① yi∗(w⃗⋅xi⃗+b)−1>0y_i*(\vec{w}·\vec{x_i}+b)-1>0yi​∗(w⋅xi​​+b)−1>0，λi=0\lambda_i=0λi​=0;

② yi∗(w⃗⋅xi⃗+b)−1=0y_i*(\vec{w}·\vec{x_i}+b)-1=0yi​∗(w⋅xi​​+b)−1=0，λi≠0\lambda_i≠0λi​=0。

同时我们也推导出λi≥0\lambda_i≥0λi​≥0这个条件。

根据上面的两个条件我们可以得到一些结论。

• 如果数据点在正负超平面w⃗⋅xi⃗+b±1=0\vec{w}·\vec{x_i}+b±1=0w⋅xi​​+b±1=0上，由于∣yi∣=1|y_i|=1∣yi​∣=1，所以yi∗(w⃗⋅xi⃗+b)−1=0y_i*(\vec{w}·\vec{x_i}+b)-1=0yi​∗(w⋅xi​​+b)−1=0，则属于情况②，故λi＞0\lambda_i＞0λi​＞0。

• 如果数据点不在正负超平面上w⃗⋅xi⃗+b±1=0\vec{w}·\vec{x_i}+b±1=0w⋅xi​​+b±1=0上，则属于情况①，所以λi=0\lambda_i=0λi​=0。而将λi=0\lambda_i=0λi​=0代入可得λi(yi∗(w⃗⋅xi⃗+b)−1)=0\lambda_i(y_i*(\vec{w}·\vec{x_i}+b)-1)=0λi​(yi​∗(w⋅xi​​+b)−1)=0。

上述推导说明，我们在计算超平面权重值www时只需要用到支持向量（在正负超平面上的数据点），而不需要非支持向量。

有了前文铺垫，我们就可以得出支持向量机SVM算法了。

① 通过下列问题求得λi\lambda_iλi​的值
max(q(λ))=max(∑i=1sλi−12∑i=1s∑j=1sλiλjyiyjxi⃗⋅xj⃗)其中λi≥0max(q(\lambda))=max(\sum_{i=1}^s{\lambda_i}-\frac{1}{2}\sum_{i=1}^{s}\sum_{j=1}^s\lambda_i\lambda_jy_iy_j\vec{x_i}·\vec{x_j})\\其中\lambda_i≥0 max(q(λ))=max(i=1∑s​λi​−21​i=1∑s​j=1∑s​λi​λj​yi​yj​xi​​⋅xj​​)其中λi​≥0
② 根据KKT条件
w⃗=∑i=1sλiyixi⃗\vec{w}=\sum_{i=1}^s\lambda_iy_i\vec{x_i} w=i=1∑s​λi​yi​xi​​
可以求出w⃗\vec{w}w

标题

③ 根据yi∗(w⃗⋅xi⃗+b)−1=0y_i*(\vec{w}·\vec{x_i}+b)-1=0yi​∗(w⋅xi​​+b)−1=0求解出bbb

升维转换与核技巧

我们看下面一个情景：

比如现在在一维x轴上有一些数据点，红色和蓝色。我们现在想要将其用一个函数（对于一维来说就是一个常量）去划分红点和蓝点。很直观地可以看出，这个是不可能的。

但是，如果上图是由二维平面图形投影到一维x轴上而产生的，我们“还原”二维平面，或许会发现不一样的世界：

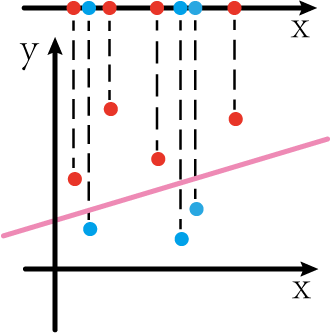
如上图，如果我们能通过某些方法将一维的数据点转化为二维的数据点，那么我们似乎可以很容易对数据点进行划分（如图中粉红色那条线）

这一过程即为升维转换。

在支持向量机中我们也可以利用这个方法。我们先回顾下优化方程：
max(q(λi))=max(∑i=1sλi−12∑i=1s∑j=1sλiλjyiyjxi⃗⋅xj⃗)其中λi≥0max(q(\lambda_i))=max(\sum_{i=1}^s{\lambda_i}-\frac{1}{2}\sum_{i=1}^{s}\sum_{j=1}^s\lambda_i\lambda_jy_iy_j\vec{x_i}·\vec{x_j})\\其中\lambda_i≥0 max(q(λi​))=max(i=1∑s​λi​−21​i=1∑s​j=1∑s​λi​λj​yi​yj​xi​​⋅xj​​)其中λi​≥0
xi⃗⋅xj⃗\vec{x_i}·\vec{x_j}xi​​⋅xj​​表示在原维度下对应向量坐标的点积。但是事实上，上述方程是无解的，所以我们可以利用核技巧进行升维变换。我们会通过一个函数T(x)T(x)T(x)进行升维变换操作，这个函数我们称之为维度转换函数。通过维度转换函数，原来的xi⃗\vec{x_i}xi​​变成了T(xi⃗)T(\vec{x_i})T(xi​​)，xj⃗\vec{x_j}xj​​变成了T(xj⃗)T(\vec{x_j})T(xj​​)。所以原问题也转换成了下式：
max(q(λi))=max(∑i=1sλi−12∑i=1s∑j=1sλiλjyiyjT(xi⃗)⋅T(xj⃗))其中λi≥0max(q(\lambda_i))=max(\sum_{i=1}^s{\lambda_i}-\frac{1}{2}\sum_{i=1}^{s}\sum_{j=1}^s\lambda_i\lambda_jy_iy_jT(\vec{x_i})·T(\vec{x_j}))\\其中\lambda_i≥0 max(q(λi​))=max(i=1∑s​λi​−21​i=1∑s​j=1∑s​λi​λj​yi​yj​T(xi​​)⋅T(xj​​))其中λi​≥0
事实上，这里我们既可以通过xi⃗、xj⃗\vec{x_i}、\vec{x_j}xi​​、xj​​写出T(xi⃗)、T(xj⃗)T(\vec{x_i})、T(\vec{x_j})T(xi​​)、T(xj​​)，然后再进行点积操作，也可以直接令K(xi⃗,xj⃗)=T(xi⃗)⋅T(xj⃗)K(\vec{x_i},\vec{x_j})=T(\vec{x_i})·T(\vec{x_j})K(xi​​,xj​​)=T(xi​​)⋅T(xj​​)，然后进行计算。这两者的区别在于，后者是直接将xi⃗⋅xj⃗\vec{x_i}·\vec{x_j}xi​​⋅xj​​看成一个未知数整体代入计算。而这里的K(xi⃗,xj⃗)K(\vec{x_i},\vec{x_j})K(xi​​,xj​​)即为核函数。其一般表达式如下：
K(xi⃗,xj⃗)=(c+xi⃗⋅xj⃗)dK(\vec{x_i},\vec{x_j})=(c+\vec{x_i}·\vec{x_j})^d K(xi​​,xj​​)=(c+xi​​⋅xj​​)d
那么参数c和dc和dc和d都有什么作用呢？

对于相同的ddd，不同的ccc来说，ccc可以控制低次项的存在与否，以及低次项的系数；

对于相同的ccc，不同的ddd来说，ddd的大小决定了最高维度大小。

除此之外，核函数还可以由多个核函数线性组合而成，比如：K1′(xi⃗,xj⃗)+K2′(xi⃗,xj⃗)K_1'(\vec{x_i},\vec{x_j})+K_2'(\vec{x_i},\vec{x_j})K1′​(xi​​,xj​​)+K2′​(xi​​,xj​​)

也有一种比较特殊的核函数，即将二维转化成无穷维。这个核函数是高斯核函数(RBF)，其公式如下：
K(xi⃗,xj⃗)=e−γ∣∣xi⃗−xj⃗∣∣2K(\vec{x_i},\vec{x_j})=e^{-\gamma||\vec{x_i}-\vec{x_j}||^2} K(xi​​,xj​​)=e−γ∣∣xi​​−xj​​∣∣2

软间隔

前文中解释过软硬间隔的概念，下面我们详细讨论下。

如上图，有个点A违反了约束条件，在黄线和黑线之内。

我们知道硬间隔约束条件为yi∗(w∗⃗⋅xi⃗+b∗)−1≥0y_i*(\vec{w^*}·\vec{x_i}+b^*)-1≥0yi​∗(w∗⋅xi​​+b∗)−1≥0。如果点A违背约束条件，则点A满足式子ya∗(w∗⃗⋅xa⃗+b∗)−1＜0y_a*(\vec{w^*}·\vec{x_a}+b^*)-1＜0ya​∗(w∗⋅xa​​+b∗)−1＜0。我们想要把不等式转化为等式，则需要一个ϵa\epsilon_aϵa​来衡量误差，式子如下：
ϵa=1−ya∗(w∗⃗⋅xa⃗+b∗)\epsilon_a=1-y_a*(\vec{w^*}·\vec{x_a}+b^*) ϵa​=1−ya​∗(w∗⋅xa​​+b∗)
所以软间隔优化问题如下：

在gi(w,b)=yi∗(w⃗⋅xi⃗+b)−1＞0g_i(w,b)=y_i*(\vec{w}·\vec{x_i}+b)-1＞0gi​(w,b)=yi​∗(w⋅xi​​+b)−1＞0和max(0,1−ya∗(w∗⃗⋅xa⃗+b∗))max(0,1-y_a*(\vec{w^*}·\vec{x_a}+b^*))max(0,1−ya​∗(w∗⋅xa​​+b∗))条件下，

求∣∣w⃗∣∣22+C∑i=1sϵi求\frac{||\vec{w}||^2}{2}+C\sum_{i=1}^s{\epsilon_i}求2∣∣w∣∣2​+C∑i=1s​ϵi​的最小值。

我们可以和之前的硬间隔优化问题进行比对：

在gi(w,b)=yi∗(w⃗⋅xi⃗+b)−1＞0g_i(w,b)=y_i*(\vec{w}·\vec{x_i}+b)-1＞0gi​(w,b)=yi​∗(w⋅xi​​+b)−1＞0条件下，

求∣∣w⃗∣∣22求\frac{||\vec{w}||^2}{2}求2∣∣w∣∣2​的最小值。

事实上，软间隔相比于硬间隔的最大差别是在于多了一项
C∑i=1sϵiC\sum_{i=1}^s{\epsilon_i} Ci=1∑s​ϵi​
这一项的意思就是，将所有的误差∑i=1sϵi\sum_{i=1}^s{\epsilon_i}∑i=1s​ϵi​考虑到优化问题中，这样求最小值的时候也能够起到减少误差的作用。而常数CCC是我们人为规定的，它起到调节误差容忍度的作用。

• CCC越大，说明对ϵi\epsilon_iϵi​的容忍度越小，也就是最终算出来的结果中产生的误差越少；
• CCC越小，说明对ϵi\epsilon_iϵi​的容忍度越大，也就是最终算出来的结果中产生的误差越大；