在棋盘上放置8个皇后，使它们不同行，不同列，不同对角线。N皇后问题是8皇后问题的拓展。

下面以四皇后问题为例描述解题过程：

从第一行开始放置皇后，第1行从左到右有4种方案，产生4个子结点；

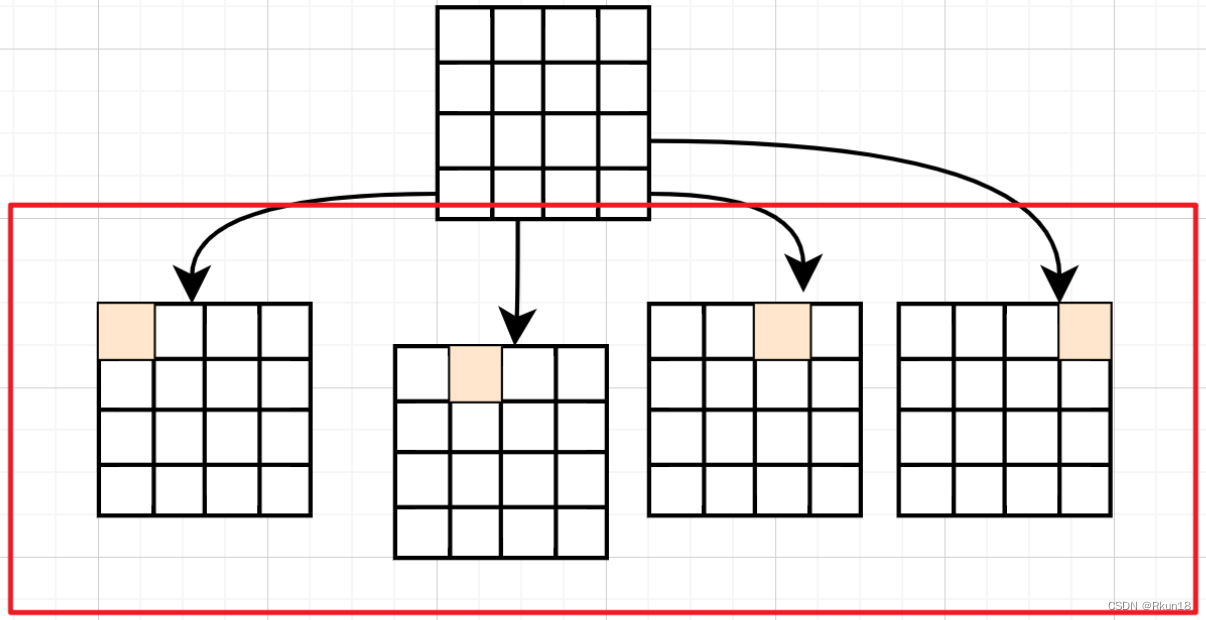
第二行，排除同列和斜线，扩展新的子结点（这里不用排除同行，因为一直向下走，始终不在同一行），如此往复，直到得出可行的方案。

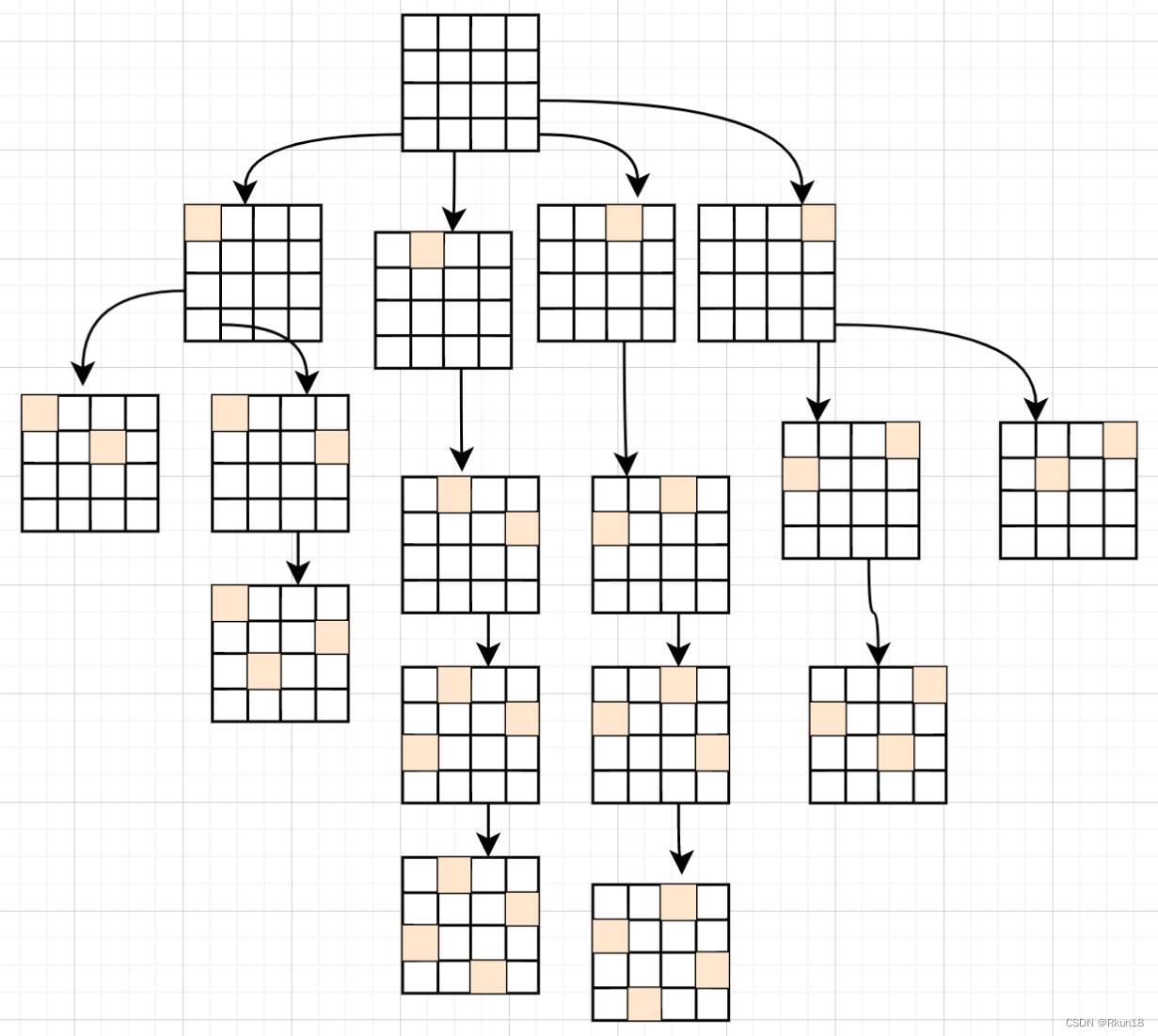
关键问题：在拓展结点时如何去掉不符合条件的子节点？

设左上角坐标(0,0),已经放好的皇后坐标为(i,j),不同行，不同列，不同斜线的新皇后坐标为(r,c),它们的关系为：

1. 横向，不同行：i！=r;

2. 纵向,不同列: j!=c;

3. 斜对角:从(i,j)向斜对角走a步，新坐标(r,c)有四种情况，即(i-a,j-a),(i+a,j-a),(i-a,j+a),(i+a,j+a),所以综合起来看，新皇后位置满足|i-r|!=|j-c|。

数组设置：

  static int col[] = new int[12];//每一列皇后放置的行号static int n, tot; //n皇后,tot能够实现的数量

检查放置的新皇后是否和之前的皇后有冲突：

 static boolean check(int c, int r) {for (int i = 0; i < r; i++) {if (col[i] == c || Math.abs(col[i] - c) == Math.abs(i - r)) {return false;}}return true;}

一层一层放置皇后：

 static void dfs(int r) {if (r == n) {//达到n皇后 数量加1tot++;return;}for (int c = 0; c < n; c++) {if (check(c, r)) {col[r] = c;dfs(r + 1);}}}

完整代码：

package search;import java.util.Arrays;
import java.util.Scanner;public class hdu2553 {static int col[] = new int[12];//每一列static int n, tot; //n皇后,tot能够实现的数量public static void main(String[] args) {Scanner sc = new Scanner(System.in);int ans[] = new int[12];for (n = 0; n <= 10; n++) {Arrays.fill(col, 0);tot = 0;dfs(0);ans[n] = tot;}while (sc.hasNext()) {n = sc.nextInt();if (n == 0) return;System.out.println(ans[n]);}}//检查是否和已经放好的皇后有冲突static boolean check(int c, int r) {for (int i = 0; i < r; i++) {if (col[i] == c || Math.abs(col[i] - c) == Math.abs(i - r)) {return false;}}return true;}static void dfs(int r) {if (r == n) {//达到n皇后 数量加1tot++;return;}for (int c = 0; c < n; c++) {if (check(c, r)) {col[r] = c;dfs(r + 1);}}}
}

在vjudge上测试：

vjudge题目链接：

N皇后问题 - HDU 2553 - Virtual Judge