Matrix Animation and Polar Decomposition
理论还是要和实际结合,矩阵分解有各种各样的形式,而根据实际用途会有不同的解法。这篇论文很不错,起因是pbrt里面的trs分解:

一开始不太理解,按照我的想法,RS矩阵,它的转置是(RS)T
两者相乘,就是SIS = S^2,按理说就求出了scale矩阵,然后再求出R矩阵即可。 查阅了一下论文:

一个复合矩阵可以很容易拆出投影P和平移T,主要是M,由RS复合。
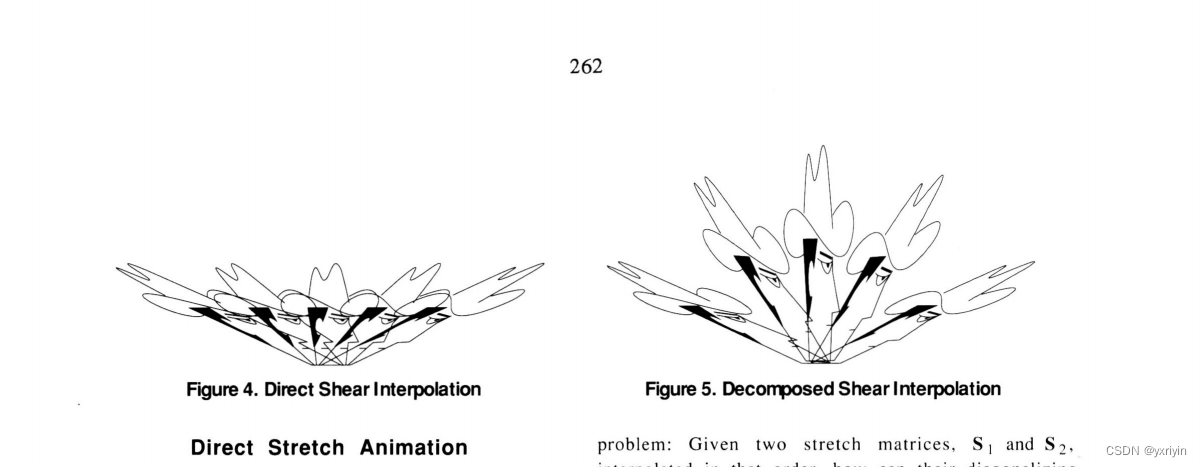
如果不拆解,直接插值,那么效果是这样的:
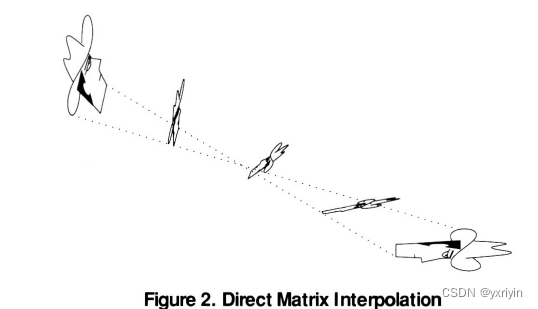
显然,这不是我们想要的插值效果。
然后便是我们需要理解的RS问题,对于任何一个物体,单独看的话,确实是可以进行RS分解。
但是,如果物体有层级关系,那么就有可能弄出一个SR的矩阵,比如父亲是缩放,儿子是旋转,就会这样:
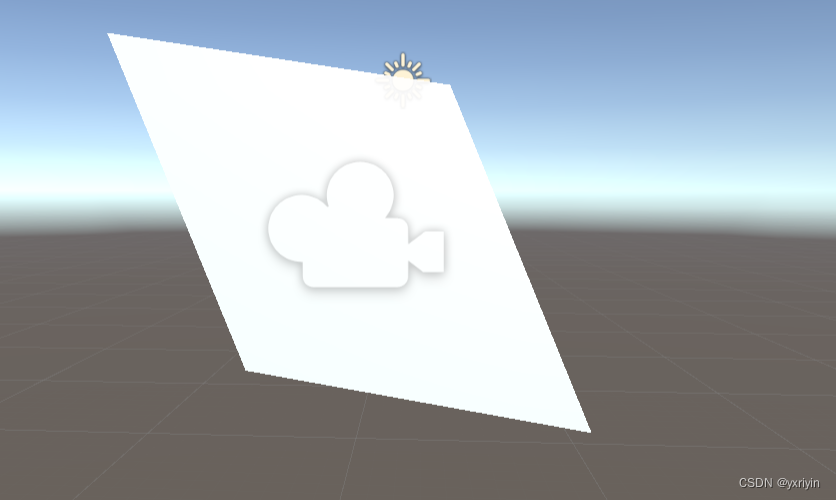
这叫做shear (剪切),可以用旋转和缩放模拟出来的效果(先旋转,在缩放),这是无法通过RS矩阵来表示的。
把他拖到世界根节点,会变成:
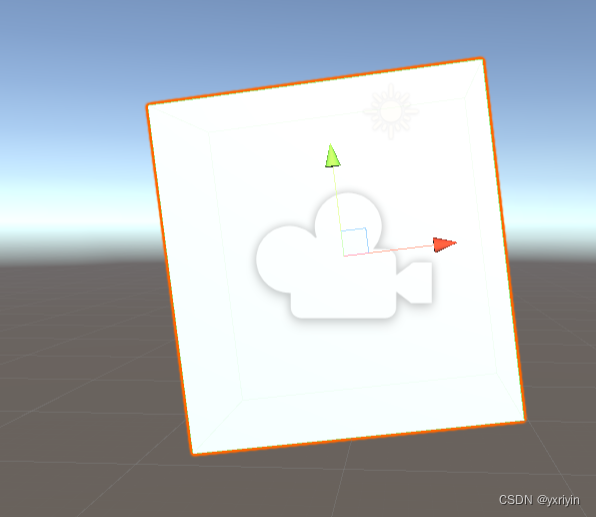

这里讲了三种分解分别的算法,其中奇异值分解算法最复杂。
后面开始对比各类分解的优缺点:
奇异值分解算的复杂,而且分解出来的正交矩阵可用性不足(对于动画矩阵而言)。举个例子,一个旋转矩阵的奇异值分解,可以变成无数种的两个旋转的组合。
而且输入的微小差别会导致产生完全不同的正交基。
再考虑这样的情况:

毫无疑问是合理的分解,但缺产生了和实际世界毫无意义的信息。
QR分解是唯一的,而且相对稳定。计算也算迅速,但是,它的正交矩阵似乎没有任何实际的物理意义。

这是什么意思呢,就是说如果矩阵M代表的是旋转和缩放,那么其实我们希望它是坐标系无关的。也就是说,换了个坐标系,旋转依然是旋转,缩放依然是缩放。但是,通过QR分解之后,我们发现,本来的下三角阵他就不是下三角阵了。这和我们的预期不符合。
也就是说,如果物体是先旋转后缩放,那么QR分解将无法把旋转和缩放分离出来。它只能处理先缩放后旋转的情况。

而极分解则是唯一的,而且是坐标系无关的,而且是容易计算的。而且Q是最接近M的正交矩阵。


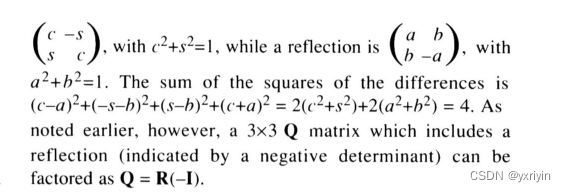
这里也非常有意思,如果M的行列式为正,那么Q就是一个纯旋转,如果M行列式为负,那么我们需要增加一个反射矩阵。也许最好排除反射矩阵,但那样的话我们很难找到和它最近的旋转,因为每个旋转和任何反射之间的距离是固定的。例如2D旋转,它和它反射的距离永远是4.
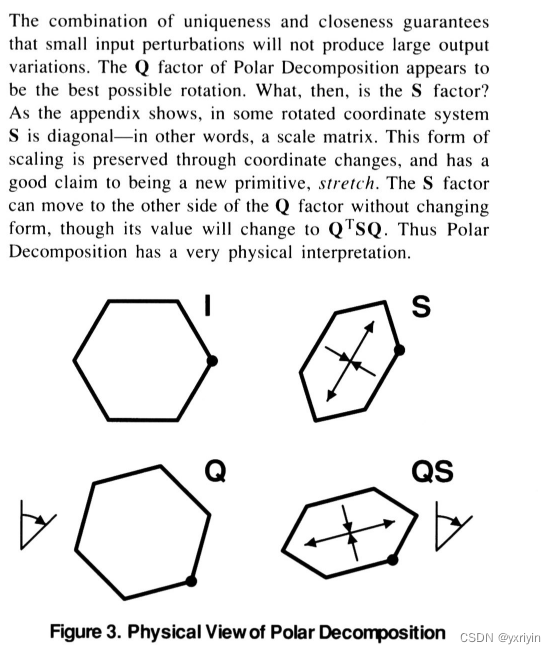
这里主要证明极分解的两种形式
参考:https://zh.wikipedia.org/zh-hans/%E6%9E%81%E5%88%86%E8%A7%A3

 其实很好证明
其实很好证明
M=QS=QSQ^-1Q 令新的S=QSQ^-1即可。刚好是旋转矩阵,所以自然可逆就是转置。
所以极分解确实有很强的物理性质。

极分解在剪切上表现不好。

这里的意思是我们继续对S进行谱分解,为了保证U1和U2尽量接近,这样我们就可以让输入的变化干扰最小。后续还有不少内容,主要是怎么选择U1,U2,Un的问题,等需要用到再说吧。
