红黑树的性质：

首先记住它的性质：

在增删节点时需要调整满足性质

1、根节点是黑色的;

2、如果一个节点是红色的，则它的两个孩子结点是黑色的;

3、对于每个结点，从该结点到其所有后代叶结点的简单路径上，均包含相同数目的黑色结点;

4、每个叶子结点都是黑色的(此处的叶子结点指的是空结点);

对颜色进行定义：

//我们用枚举表示表示出两种颜色  
//枚举默认第一个参数 BLACK 为 0 ，第二个参数 RED 为 1；
enum COLOR {BLACK,RED
};

红黑树的节点表示：

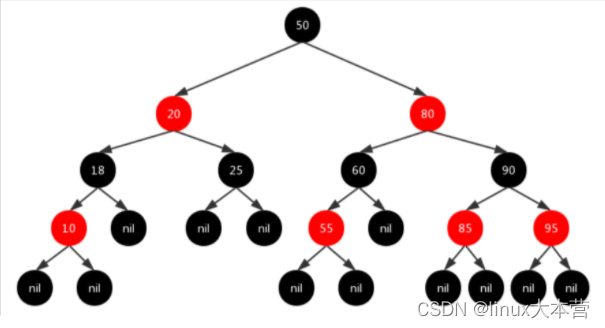
 看图说节点

红黑树的节点参数，

一个指向上面的节点定义为_parent

一个指向左边的节点的节点指针 _left

一个指向右边的 _right

一个pair类型的值

一个颜色的识别

当然这么写参数那得来个构造函数了，“细节”。

template
struct RBNode {//各个节点RBNode* _parent;RBNode* _left;RBNode* _right;//key-valuepair _kv;//颜色COLOR _color;RBNode(const pair& kv = pair()):_parent(nullptr), _left(nullptr), _right(nullptr), _kv(kv)//新申请的节点定义为RED，黑色的加入，会导致其他所有路径的黑色都遭到破坏；, _color(RED) {}
};

对树的类进行定义：

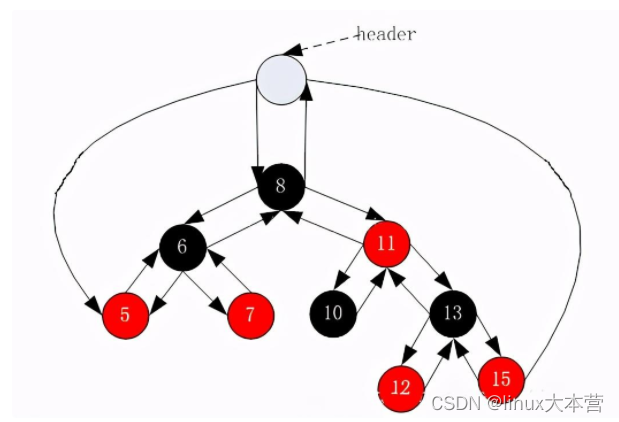
 红黑树的头节点——header

指向如图上图：具体下面再写

template
class RBTree {
public://类型定义,用Node表示RBNodetypedef RBNode Node;RBTree():_header(new Node) {//创建空树_header->_left = _header->_right = _header;}
private:Node* _header;
};

红黑树的插入：

当插入c节点时，为了满足性质，需要对节点进行调整，为了保证调整最优；

如果插入节点的父节点（u）和叔叔节点（u）为红色，那么只需要改变叔叔节点（u）和父节点（p）颜色为黑色，祖父节（g）为黑色即可；

当然如果祖父节点（g) 为根节点，再把其变为黑色；

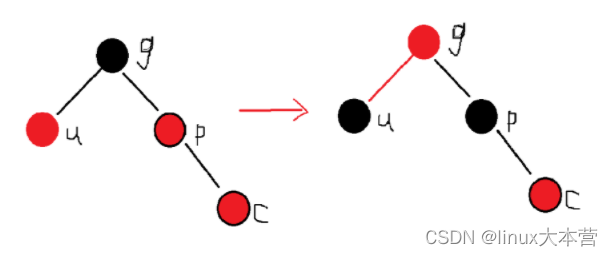
不是根节点，向上调整；

相关视频推荐

红黑树在Linux内核中的3种场景（红黑树证明，进程管理cfs，内存管理，epoll）

5种红黑树的用途，从应用到内核场景的优缺点

8个方面完善linux c/c++开发，再也不用全网搜刮了

免费学习地址：c/c++ linux 服务器开发/后台架构师

需要C/C++ Linux服务器架构师学习资料加群812855908（资料包括C/C++，Linux，golang技术，Nginx，ZeroMQ，MySQL，Redis，fastdfs，MongoDB，ZK，流媒体，CDN，P2P，K8S，Docker，TCP/IP，协程，DPDK，ffmpeg等） 

 结构右旋：

写一个左旋的操作，在树结构变化时可高效的改变保证结构性质；

如果

当出现情况1：

插入节点为c，当它的叔叔节点为黑色，或者叔叔节点不存在，操作相同；

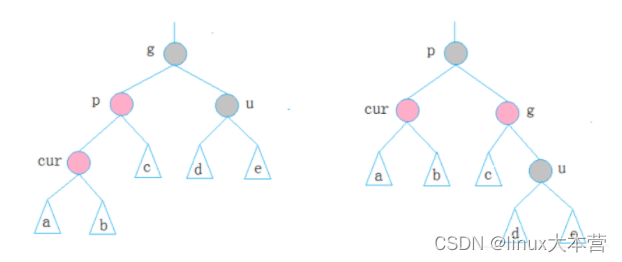
记录三个节点，只有这三个节点指向变化；
由图：
用parent表示g，
用subL表示p，
用subLR表示p的右子节点即c；
用pparent表示g的父节点；//		  parent//	subL//			subLR	void RotateR(Node* parent) {Node* subL = parent->_left;Node* subLR = subL->_right;//改变节点指向：subL->_right = parent;parent->_left = subLR;//如果存在父节点存在，如果为nullptr则没有父节点；if (subLR)subLR->_parent = parent;//判断根if (parent == _header->_parent) {_header->_parent = subL;subL->_parent = _header;}//不是根else {Node* pparent = parent->_parent;subL->_parent = pparent;if (pparent->_left == parent)pparent->_left = subL;elsepparent->_right = subL;}//先要将parent的父节点赋值出去，才能改变paremt的父节点；parent->_parent = subL;}

结构左旋：

如图顺序（未画完全，子节点仍然有且满足性质）

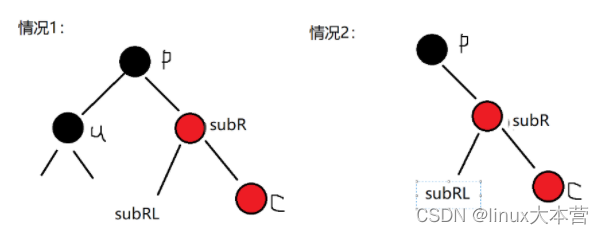
记录三个节点，只有这三个节点指向变化；（操作和右旋思路相同）
由图：
用pparent表示p的父节点；//			parent//					subR//			subRL				void RotateL(Node* parent) {Node* subR = parent->_right;Node* subRL = subR->_left;subR->_left = parent;parent->_right = subRL;if (subRL) {subRL->_parent = parent;}if (_header->_parent == parent) {_header->_parent = subR;subR->_parent = _header;}else {Node* pparent = parent->_parent;subR->_parent = pparent;if (pparent->_left == parent)pparent->_left = subR;elsepparent->_right = subR;}parent->_parent = subR;}

头节点指向的左右节点：

如图：header头节点指向最左最右的节点；

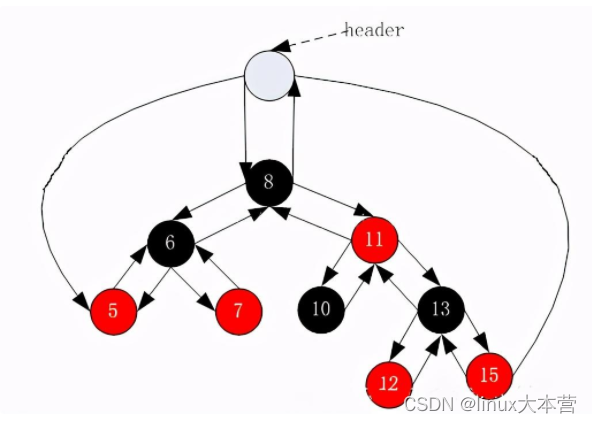
 找红黑树的最左节点：

	//最左节点Node* leftMost() {Node* cur = _header->_parent;while (cur && cur->_left) {cur = cur->_left;}return cur;}

找红黑树的最右节点：

//最右节点Node* rightMost() {Node* cur = _header->_parent;while (cur && cur->_right) {cur = cur->_right;}return cur;}

红黑树的插入情况分析：

情况1：插入节点的父节点颜色为黑色；

处理1：直接插入;

情况2：插入节点的父节点为红色，叔叔节点存在且为红色；

处理2：插入后叔叔节点和父节点颜色变黑，祖父节点颜色变红，向上遍历查看情况；

情况3：父节点为红色，叔叔节点存在为黑色或不存在，插入节点为父节点的左子树，父节点为祖父节点的左子树；

处理3：进行结构右旋操作（RotateR）；

情况4：和情况3的结构调整相反父节点为红色，叔叔节点存在为黑色或不存在，插入节点为父节点的右子树，父节点为祖父节点的右子树；

处理4：进行结构左旋操作（RotateL）；

情况5：和情况6结构调整相反父节点为红色，叔叔节点存在为黑色或不存在，插入节点为父节点的左子树，父节点为祖父节点的右子树；

处理5：先以父节点为根，先右旋操作（RotateR），再以祖父节点为根，左旋操作（RotateL）；

情况6：父节点为红色，叔叔节点存在为黑色或不存在，插入节点为父节点的右子树，父节点为祖父节点的左子树；

处理6：先以父节点为根，左旋操作（RotateL），再以祖父节点为根，右旋操作（RotateR）；

上图:（个情况）

情况1：

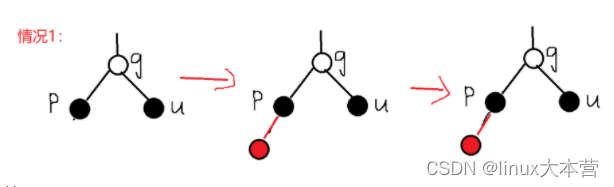
 情况2：

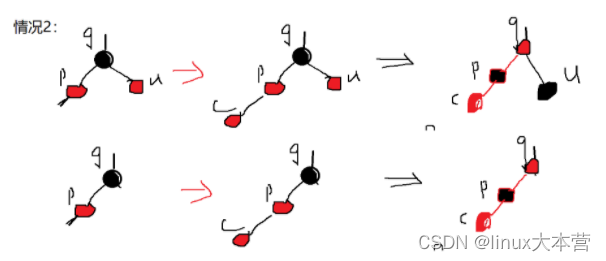
 情况3：

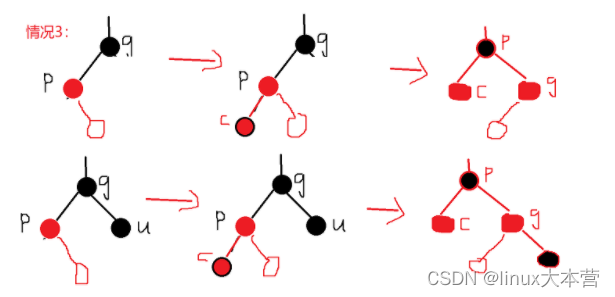
 情况4：

和情况3相反，自己画去；

情况5：

情况6相反，自己画去；

情况6

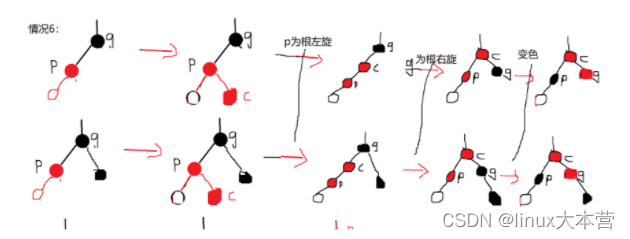
上代码：

	//插入bool insert(const pair& kv) {//1.搜索树颜色//空树：_header->parent:nullptrif (_header->_parent == nullptr) {//创建根节点Node* root = new Node(kv);_header->_parent = root;root->_parent = _header;_header->_left = _header->_right = root;//根节点是黑色root->_color = BLACK;return true;}//从根节点开始搜索//正常插入Node* cur = _header->_parent;Node* parent = nullptr;while (cur) {parent = cur;//和key值进行比较//kv： pair, key:pair.firstif (cur->_kv.first == kv.first) {//key值存在，不允许插入return false;}else if (cur->_kv.first > kv.first) {//向小的找,左子树去找cur = cur->_left;}else {//向大的找,右子树去找cur = cur->_right;}}//找到了//创建待插入节点cur = new Node(kv);if (parent->_kv.first > cur->_kv.first)parent->_left = cur;//比较大小，插在左右那个位置；elseparent->_right = cur;cur->_parent = parent;//2.调整结构或者修改颜色//判断是否至少有三层；while (cur != _header->_parent && cur->_parent->_color == RED) {parent = cur->_parent;Node* gfather = parent->_parent;//可能出现情况6，情况3if (gfather->_left == parent) {Node* uncle = gfather->_right;//情况2：uncle存在，并且都是红色if (uncle && uncle->_color == RED) {parent->_color = uncle->_color = BLACK;gfather->_color = RED;//继续向上更新cur = gfather;}//else {cout << "Rotate" << endl;//双旋结构//情况6：if (cur == parent->_right) {RotateL(parent);swap(cur, parent);}
//经过第一次左旋后，情况6 与情况3 只有cur节点和父节点的指向不一样，
//经过swap两者后，接下来操作相同都为右旋；RotateR(gfather);parent->_color = BLACK;gfather->_color = RED;break;}}else {//gfather->_right=parent的情况；//情况4，情况5,；//处理与情况3，情况6相反；Node* uncle = gfather->_right;//uncle存在，且都是红色，最简if (uncle && uncle->_color == RED) {parent->_color = uncle->_color = BLACK;gfather->_color = RED;cur = gfather;}//情况3：uncle不存在，或者uncle存在为黑色//双旋结构else {//		gfather//	uncle    	parent  //			 cur//if (cur == parent->_left) {RotateR(parent);swap(cur, parent);}RotateL(gfather);parent->_color = BLACK;gfather->_color = RED;break;}}}//根节点的颜色改成黑的；_header->_parent->_color = BLACK;//更新header左右指向_header->_left = leftMost();_header->_right = rightMost();}

中序遍历进行打印：

//对中序遍历进行封装：void inorder() {_inorder(_header->_parent);cout << endl;}//使用递归从叶子节点开始；//1.打印最左节点，//2.打印此节点//3.打印右节点void _inorder(Node* root) {if (root) {_inorder(root->_left);cout << root->_kv.first << "--->" << root->_kv.second << endl;_inorder(root->_right);}}

判断是否满足红黑树的性质：

	//红黑树：//1.根：黑色//2.每条路径黑色个数相同//3.红色不能连续bool isBalance() {if (_header->_parent == nullptr)return true;//只有头节点也是满足红黑树Node* root = _header->_parent;//1.判断根节点的颜色if (root->_color == RED)return false;//统计一条路劲的黑色节点个数int bCount = 0;Node* cur = root;while (cur) {if (cur->_color == BLACK)++bCount;cur = cur->_left;}//遍历每一条路径int curBCount = 0;return _isBalance(root, bCount, curBCount);}bool _isBalance(Node* root, int& bCount, int curBCount) {//当root为空，一条路径遍历结束if(root == nullptr){//判断黑色节点个数是否相同if (bCount != curBCount)return false;elsereturn true;}//判断是否为黑节点if (root->_color == BLACK)++curBCount;//判断红色节点是否有连续if (root->_parent && root->_color == RED&& root->_parent->_color == RED) {cout << "data: " << root->_kv.first << "--->" << root->_kv.second << endl;return false;}return _isBalance(root->_left, bCount, curBCount) && _isBalance(root->_right,bCount, curBCount);}

完整代码如下：可直接调试

#include
#include
#include
using namespace std;
//设置颜色属性
enum COLOR {BLACK,RED
};
template
struct RBNode {//typedef bool color;//各个节点RBNode* _parent;RBNode* _left;RBNode* _right;//key-valuepair _kv;//颜色COLOR _color;RBNode(const pair& kv = pair()):_parent(nullptr), _left(nullptr), _right(nullptr), _kv(kv), _color(RED) {}
};
template
class RBTree {
public://类型定义typedef RBNode Node;RBTree():_header(new Node) {//创建空树_header->_left = _header->_right = _header;}//插入bool insert(const pair& kv) {//1.搜索树颜色//空树：_header->parent:nullptrif (_header->_parent == nullptr) {//创建根节点Node* root = new Node(kv);_header->_parent = root;root->_parent = _header;_header->_left = _header->_right = root;//根节点是黑色root->_color = BLACK;return true;}//从根节点开始搜索//正常插入Node* cur = _header->_parent;Node* parent = nullptr;while (cur) {parent = cur;//和key值进行比较//kv： pair, key:pair.firstif (cur->_kv.first == kv.first) {//key值不允许重复return false;}else if (cur->_kv.first > kv.first) {cur = cur->_left;}else {cur = cur->_right;}}//创建待插入节点cur = new Node(kv);if (parent->_kv.first > cur->_kv.first)parent->_left = cur;elseparent->_right = cur;cur->_parent = parent;//2.修改颜色或者调整结构while (cur != _header->_parent && cur->_parent->_color == RED) {parent = cur->_parent;Node* gfather = parent->_parent;if (gfather->_left == parent) {Node* uncle = gfather->_right;//1.uncle存在，并且都是红色if (uncle && uncle->_color == RED) {parent->_color = uncle->_color = BLACK;gfather->_color = RED;//继续更新cur = gfather;}else {cout << "Rotate" << endl;//双旋结构if (cur == parent->_right) {RotateL(parent);swap(cur, parent);}RotateR(gfather);parent->_color = BLACK;gfather->_color = RED;break;}}else {//gfather->_right=parent;Node* uncle = gfather->_right;//uncle存在，且都是红色，最简if (uncle && uncle->_color == RED) {parent->_color = uncle->_color = BLACK;gfather->_color = RED;cur = gfather;}//uncle不存在，或者uncle存在为黑色//双旋结构else {//		gfather//	uncle    	parent  //			 cur//if (cur == parent->_left) {RotateR(parent);swap(cur, parent);}RotateL(gfather);parent->_color = BLACK;gfather->_color = RED;break;}}}//根节点的颜色改成黑的；_header->_parent->_color = BLACK;//更新header左右指向_header->_left = leftMost();_header->_right = rightMost();}//			parent//					subR//			subRL				void RotateL(Node* parent) {Node* subR = parent->_right;Node* subRL = subR->_left;subR->_left = parent;
parent->_right = subRL;
if (subRL) {subRL->_parent = parent;
}
if (_header->_parent == parent) {_header->_parent = subR;subR->_parent = _header;
}
else {Node* pparent = parent->_parent;subR->_parent = pparent;if (pparent->_left == parent)pparent->_left = subR;elsepparent->_right = subR;
}
parent->_parent = subR;}//		  parent//		subL//			subLR	void RotateR(Node* parent) {Node* subL = parent->_left;Node* subLR = subL->_right;subL->_right = parent;parent->_left = subLR;if (subLR)subLR->_parent = parent;//判断根if (parent == _header->_parent) {_header->_parent = subL;subL->_parent = _header;}//不是根else {Node* pparent = parent->_parent;subL->_parent = pparent;if (pparent->_left == parent)pparent->_left = subL;elsepparent->_right = subL;}parent->_parent = subL;}//最左节点Node* leftMost() {Node* cur = _header->_parent;while (cur && cur->_left) {cur = cur->_left;}return cur;}//最右节点Node* rightMost() {Node* cur = _header->_parent;while (cur && cur->_right) {cur = cur->_right;}return cur;}void inorder() {_inorder(_header->_parent);cout << endl;}void _inorder(Node* root) {if (root) {_inorder(root->_left);cout << root->_kv.first << "--->" << root->_kv.second << endl;_inorder(root->_right);}}//红黑树：//1.根：黑色//2.每条路径黑色个数相同//3.红色不能连续bool isBalance() {if (_header->_parent == nullptr)return true;Node* root = _header->_parent;if (root->_color == RED)return false;//统计一条路劲的黑色节点个数int bCount = 0;Node* cur = root;while (cur) {if (cur->_color == BLACK)++bCount;cur = cur->_left;}//遍历每一条路径int curBCount = 0;return _isBalance(root, bCount, curBCount);}bool _isBalance(Node* root, int& bCount, int curBCount) {//当root为空，一条路径遍历结束if(root == nullptr){//判断黑色节点个数是否相同if (bCount != curBCount)return false;elsereturn true;}//判断是否为黑节点if (root->_color == BLACK)++curBCount;//判断红色节点是否有连续if (root->_parent && root->_color == RED&& root->_parent->_color == RED) {cout << "data: " << root->_kv.first << "--->" << root->_kv.second << endl;return false;}return _isBalance(root->_left, bCount, curBCount) && _isBalance(root->_right,bCount, curBCount);}
private:Node* _header;
};
void test() 	{RBTree rbt;int n;cin >> n;for (int i = n; i > 0; --i) {rbt.insert(make_pair(i, i));}rbt.inorder();cout << rbt.isBalance();
}
int main() {test();return 0;
}