【C++】面经101，删除有序链表中重复的元素-II，动态规划解决斐波那契，二分查找-I，二维数组中的查找，寻找峰值
创始人
2025-05-29 09:18:54

目录

1.删除有序链表中重复的元素-II

2. 动态规划解决斐波那契

3. 二分查找-I

4.二维数组中的查找

5.寻找峰值

1.删除有序链表中重复的元素-II

这个题是删除所有重复项，所以不方便用之前的方法（所有重复的项留一个），因为即使保存前一个节点依然无法解决111的情况

这个用哨兵位，这样其实就是解决之前方法的不足

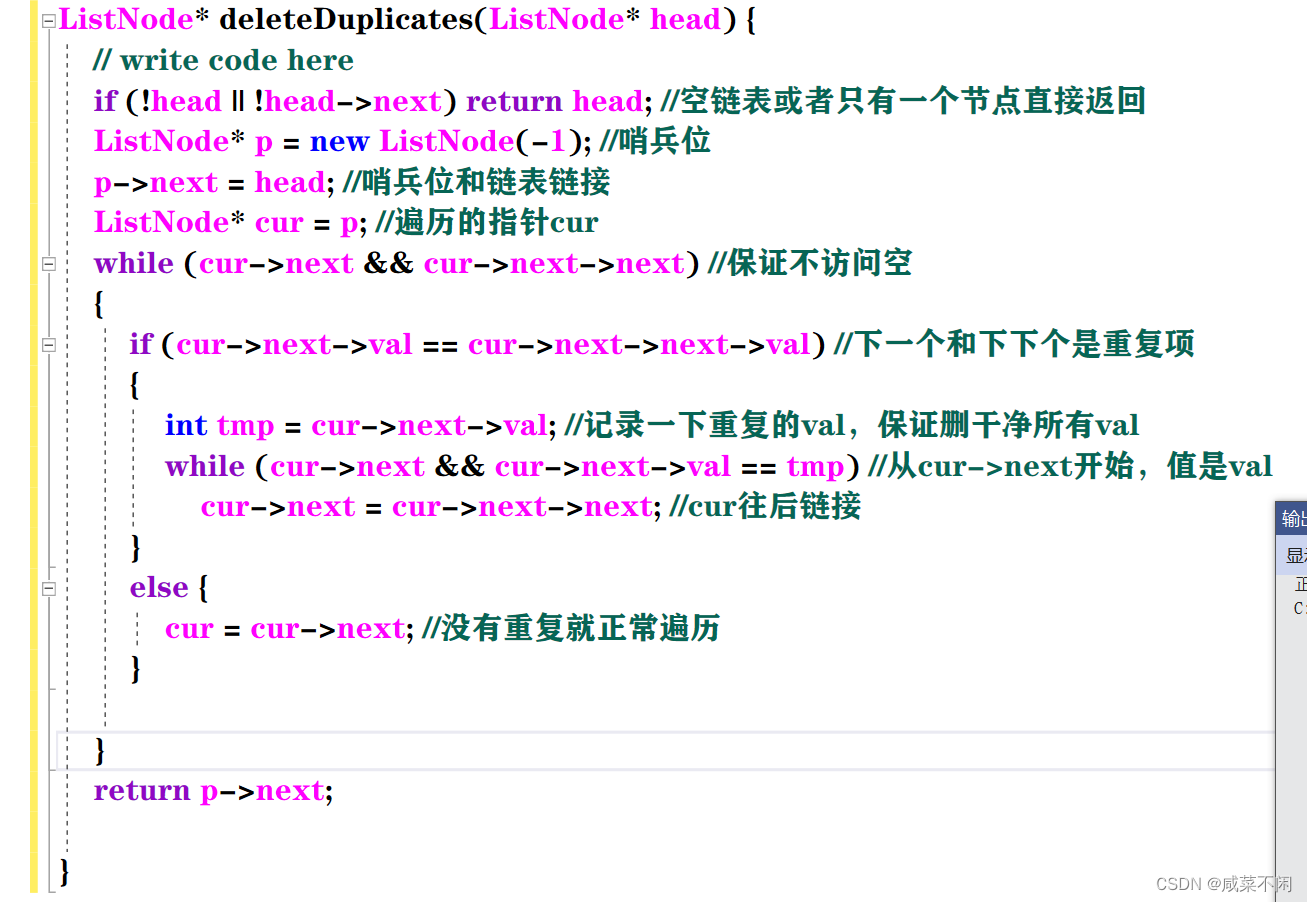
ListNode* deleteDuplicates(ListNode* head) {// write code hereif (!head || !head->next) return head; //空链表或者只有一个节点直接返回ListNode* p = new ListNode(-1); //哨兵位p->next = head; //哨兵位和链表链接ListNode* cur = p; //遍历的指针curwhile (cur->next && cur->next->next) //保证不访问空{if (cur->next->val == cur->next->next->val) //下一个和下下个是重复项{int tmp = cur->next->val; //记录一下重复的val，保证删干净所有valwhile (cur->next && cur->next->val == tmp) //从cur->next开始，值是valcur->next = cur->next->next; //cur往后链接}else {cur = cur->next; //没有重复就正常遍历}}return p->next;}

2. 动态规划解决斐波那契

动态规划要义：

把问题分解成不能再分的，无需复杂分析的子问题

确定状态

初始化

建立状态方程

最后返回末状态

class Solution {
public:int Fibonacci(int n) {int F[n + 1]; //用数组保存每个斐波那契数，节约成本，避免不必要的多次计算F[0] = 1; //初始化F[1] = 1; //初始化for (int i = 2; i < n; i++){F[i] = F[i - 1] + F[i - 2]; //状态方程的建立}return F[n - 1]; //返回末状态}
};

3. 二分查找-I

注意begin==end也可以进训话，因为只有一个数字时，begin==end，这样进循环判断一下直接返回了

  int search(vector& nums, int target) {// write code hereint begin=0,end=nums.size()-1;while(begin<=end){int mid=(begin+end)/2;if(target==nums[mid])return mid;else if(target>nums[mid])begin=mid+1;else if(target

4.二维数组中的查找

首先是我自己的思路，观察到二维数组有序

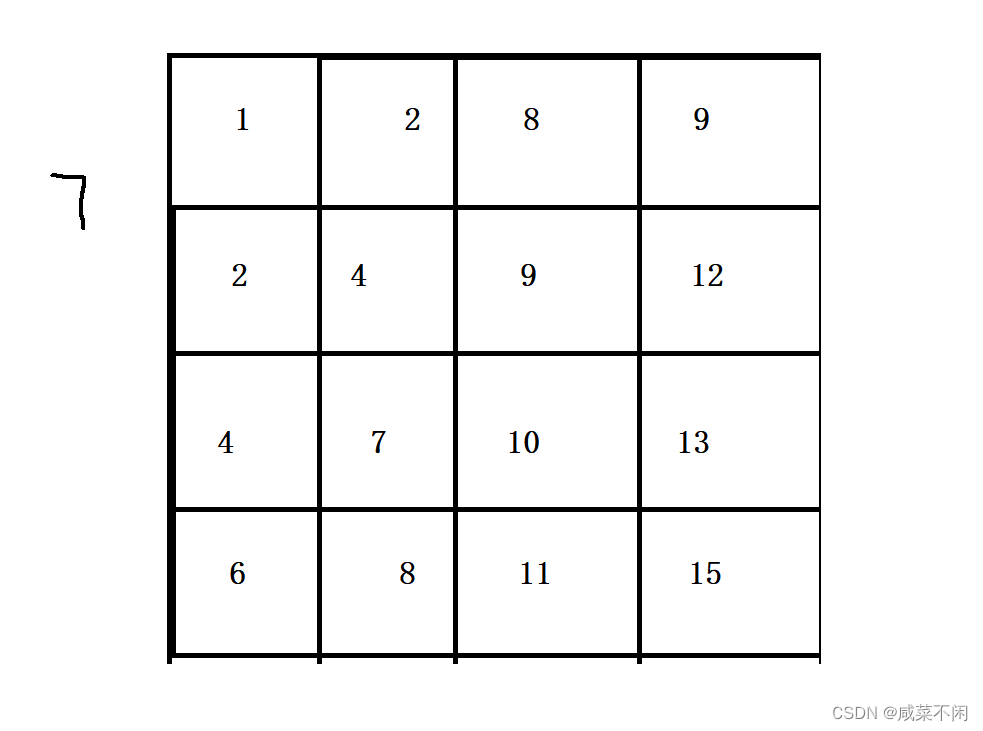
要找7肯定先和每一行的第一个元素比较，如果target比行首元素更大，那么进去那一行挨个比较，如果target更小直接返回false，如果刚好相等，那么true


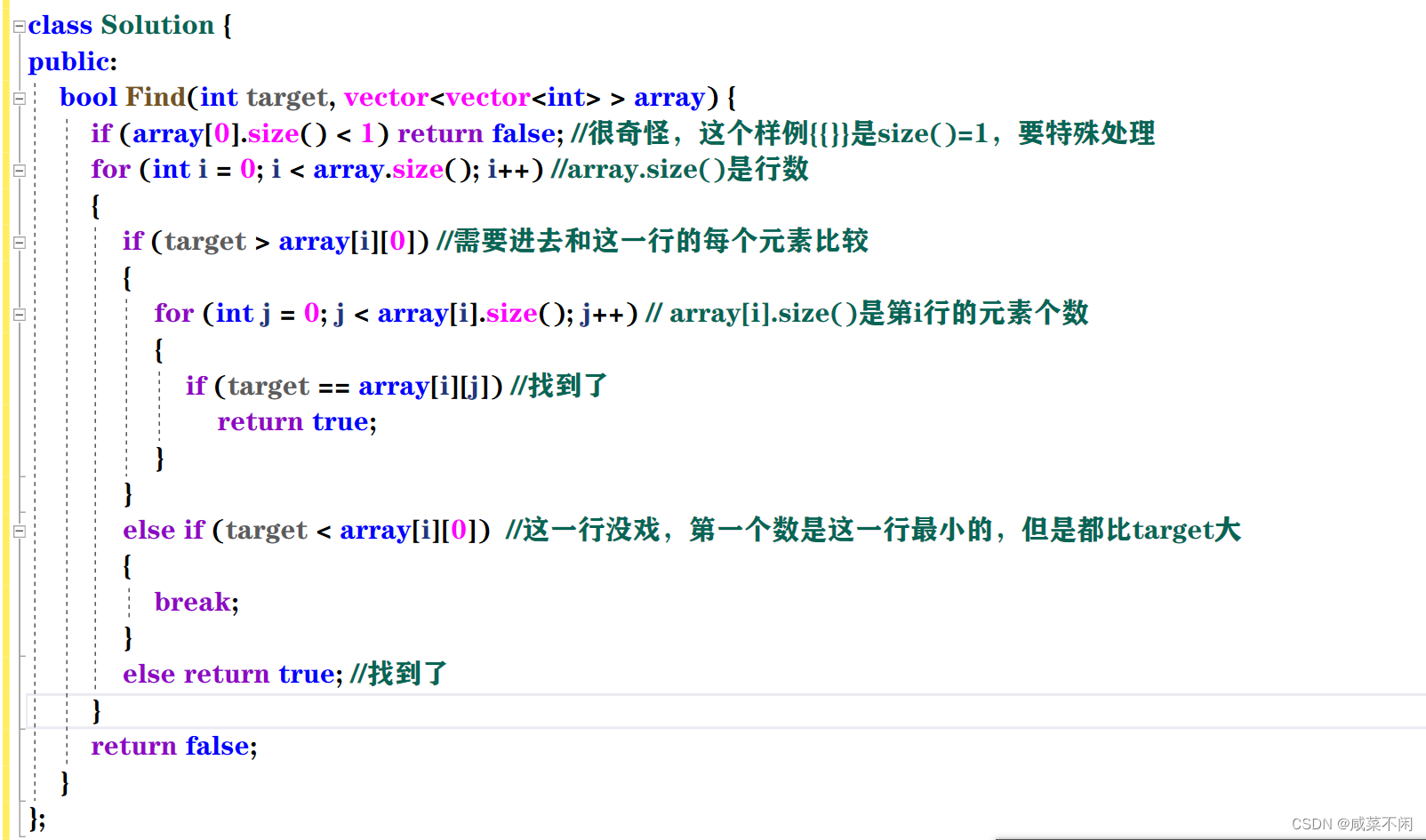
class Solution {
public:bool Find(int target, vector > array) {if (array[0].size() < 1) return false; //很奇怪，这个样例{{}}是size()=1，要特殊处理for (int i = 0; i < array.size(); i++) //array.size()是行数{if (target > array[i][0]) //需要进去和这一行的每个元素比较{for (int j = 0; j < array[i].size(); j++) // array[i].size()是第i行的元素个数{if (target == array[i][j]) //找到了return true;}}else if (target < array[i][0])  //这一行没戏，第一个数是这一行最小的，但是都比target大{break;}else return true; //找到了}return false;}
};

5.寻找峰值

两个方法，最简单的就是根据题意写

int findPeakElement(vector& nums) {// write code herefor (int i = 0; i < nums.size(); i++)  //遍历{if (i == 0) //可能第一项就是峰值{if (nums[i] > nums[i + 1]) //判断是不是峰值return i;}else if (i == nums.size() - 1) //可能最后一项是峰值{if (nums[i] > nums[i - 1]) //判断是不是return i;}else {if (nums[i] > nums[i - 1] && nums[i] > nums[i + 1])//普通位置的判断 return i;}}return -1;
}
};

时间复杂度O（n）不是很优

直接二分查找,时间复杂度O（logn）

int findPeakElement(vector& nums) {// write code hereint begin = 0, end = nums.size() - 1; //两侧while (begin < end) //不能写等号，因为相等的时候都是0，mid也是0，但是没有nums[0+1](越界）{int mid = (begin + end) / 2;if (nums[mid] < nums[mid + 1])begin = mid + 1;elseend = mid;}return begin; //随便=返回begin/end
}
};

上一篇：独家分享.YY棋牌到底有挂吗.(详细开挂教程)

下一篇：玩家必看“微乐海南麻将究竟是不是有挂”(的确有挂)

相关内容

热门资讯

2026 CES 霞光社&qu... 合作伙伴 & 招募持续进行中无论您是希望登上Panel畅谈前沿观点的思想者，还是希望成为我们探展镜头...
快手开盘股价直线下跌，黑灰产攻... 12月23日，港股开盘，快手（1024.HK）股价直线下跌。截至发稿，股价62.9港元，跌5.7%。...
你们四川人的嘴太严了 你究竟还藏了多少秘密？听说斯基在乐山，波旁斯基张口就来：乐山美食经济三驾马车：甜皮鸭、跷脚牛肉和钵钵...
海南板块大幅高开 12月23日早盘，海南板块大幅高开，海峡股份、海汽集团、海南发展、海南瑞泽涨停，康芝药业、海南机场、...
化工品轮番涨价 高端产能有序扩... 近期MDI、碳酸锂等化工品轮番涨价，涨价潮驱动化工板块表现活跃。其中，在能源成本、运输成本与环保压力...