一、二叉树

1.1 树

说到树，我们暂时忘记学习，来看一下大自然的树：

哈哈 以上照片是自己拍的，大家凑合看看

回归正题，那么在数据结构中，树是什么呢，通过上面的图片大家也可以理解

树是一种非线性的数据结构
像这样 ，有多个节点组成的有一定层次关系的结构，像是一颗相对于天空逆生长的一颗树，节点像是一片片树叶，黑色的线条像是树枝，而最顶上的那个节点像是树根，因此得名 树

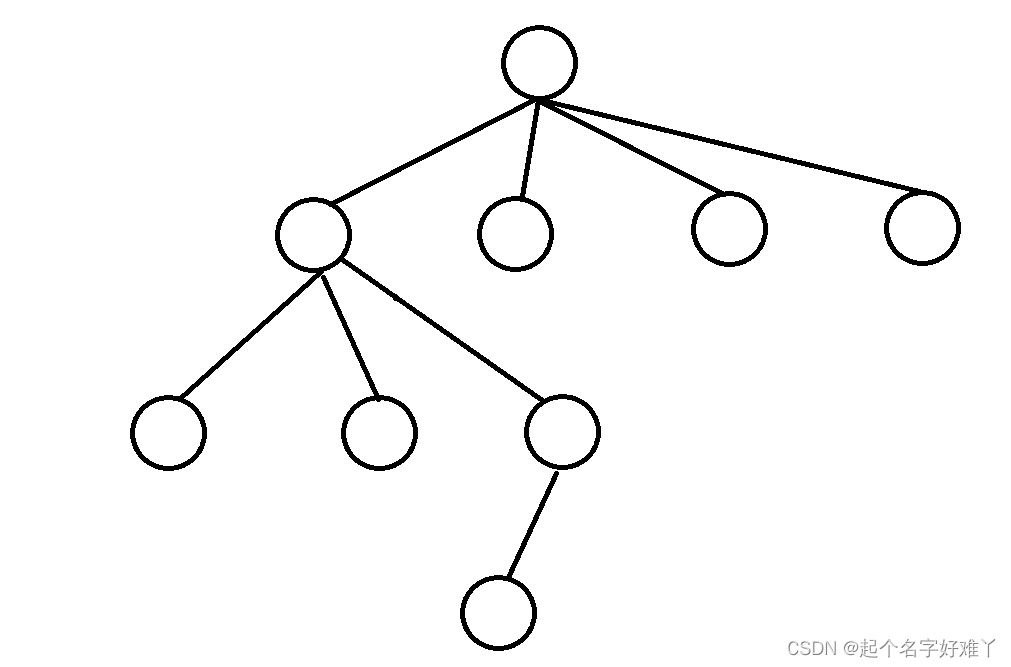
2.2 二叉树

二叉树长什么样子呢？
来看一下大自然的 “二叉树”

百度出来的图
是不是下面这个样子

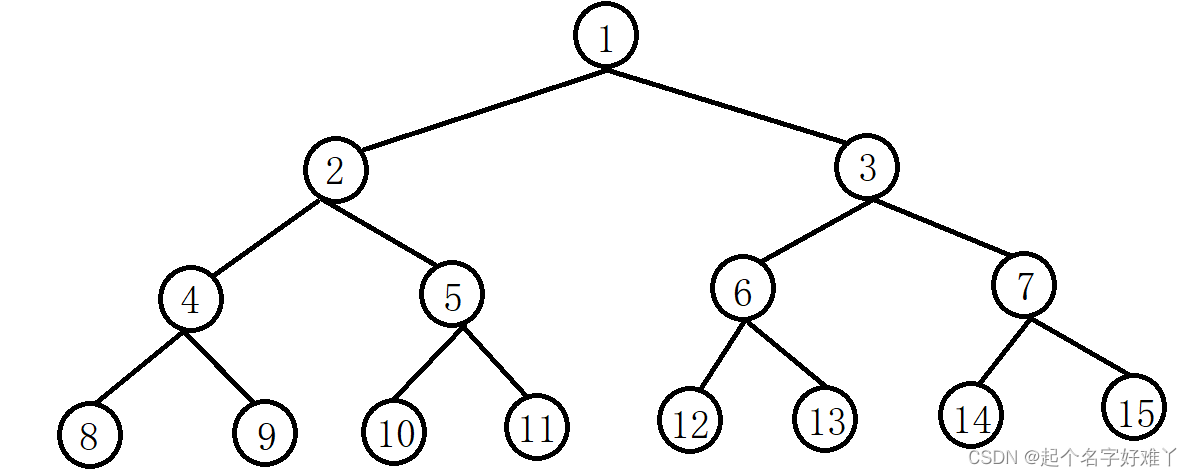
从根开始，开始分叉，每次只分两个叉，就这样一直分下去
二叉树有什么特点呢？

1.最顶上的那个节点叫做整棵树的 根节点
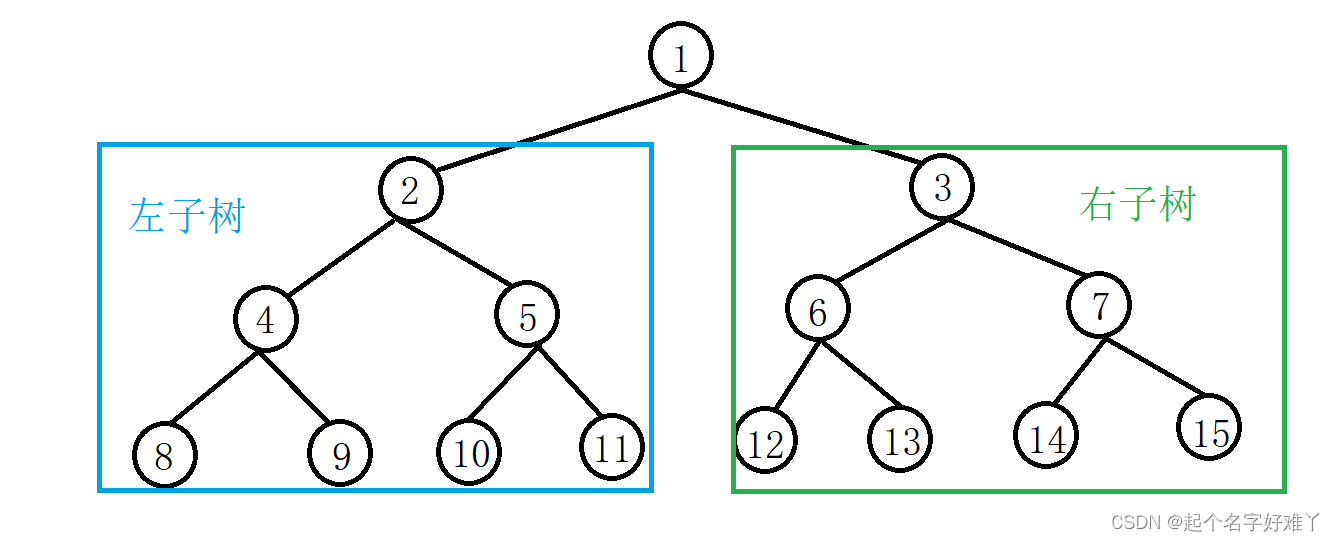
2.根据根节点可以将整棵树划分为 左右子树

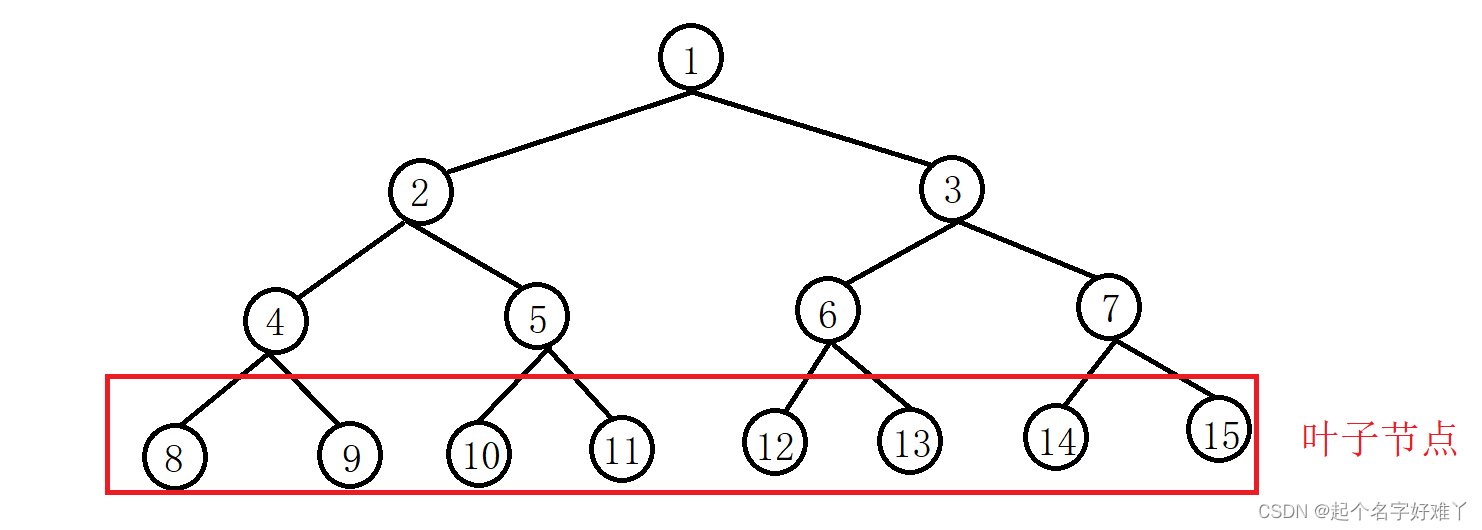
3.叶子节点，像最末端的 8~15 ，没有继续分叉的，就是叶子节点了，只要还继续有分叉的不被叫做叶子节点，叶子没法分叉了对吧

4.Parents 双亲节点(父母节点) 像 1 就是 2 、3 的 双亲节点，有时候也叫父节点，或者说，相对于 4 5 来说，2 就像是根节点一样
5. 左孩子、右孩子 ，像 4 就是 2 的左孩子节点、5 是 2 的右孩子节点
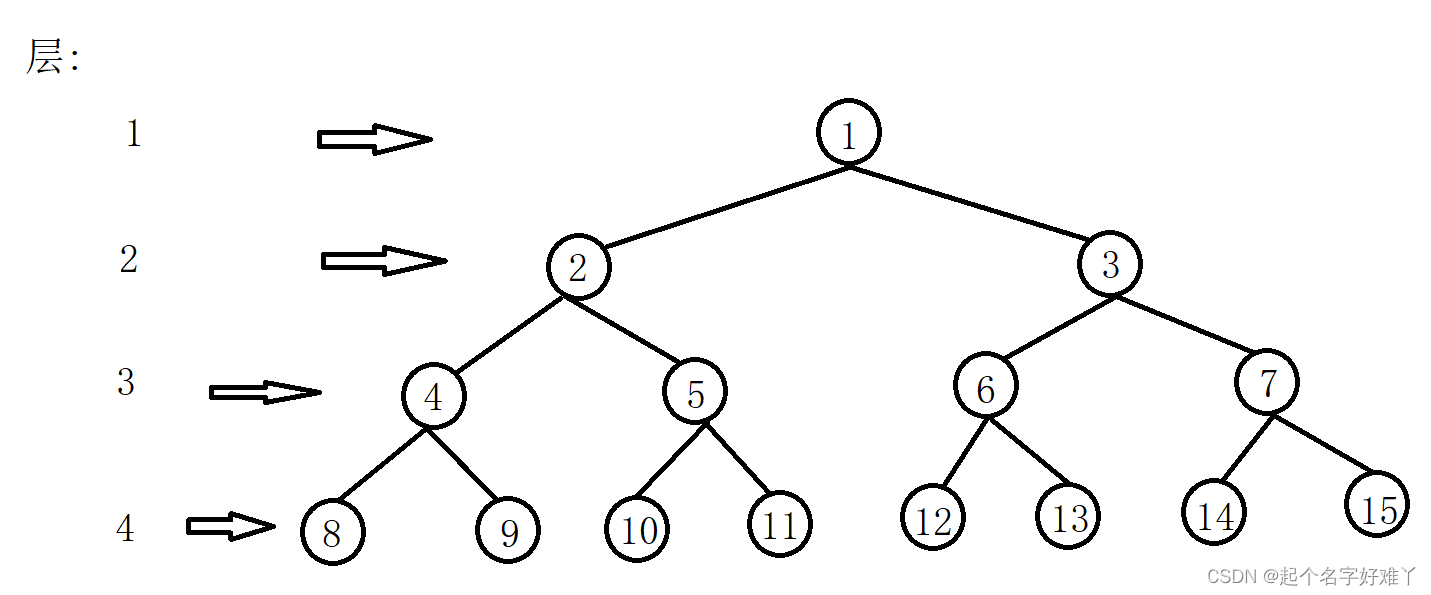
6.层：4 层

7.树的高度：每加一层 代表树的高度 + 1 像上图树的高度就是 4
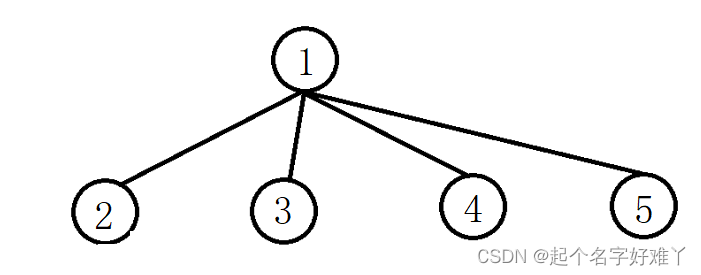
8.节点的度 ，这里的度指的是 “出度” 就是 一个 双亲节点 有几个 孩子节点 像 节点 2 的 度就是 2，而像之前说的 不是二叉树的树，像这样：节点 1 的出度就是 4

大概了解了二叉树的特点之后我们再来看一下下面这两个比较特殊的二叉树

2.2.1 满二叉树

也就是每一层的节点数都达到最大值，满满的没有空缺的，除了最后一层的叶子节点外，所有的节点都拥有两个孩子节点，就是下面这个样子

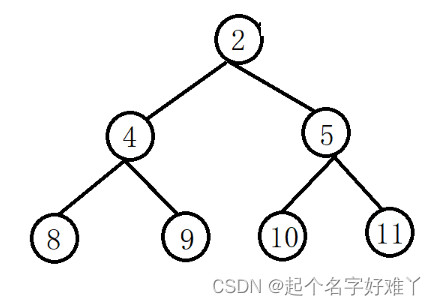
2.2.2 完全二叉树

完全二叉树，就是在满二叉树的基础上，允许每个节点不一定分两个叉，也就是说
满二叉树，除了叶子节点，其他的所有节点的度都是 2
完全二叉树，并不是所有的节点的度都是 2 ，但是 这一特定仅限定于倒数第二层的节点，例如：

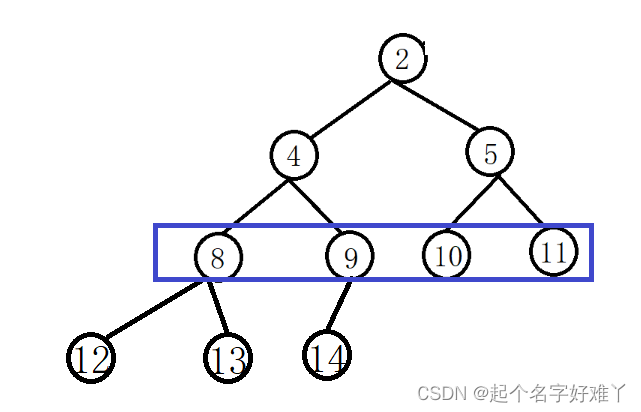
允许 节点 9 的 度 为 1 ，每个节点的子节点(左孩子、右孩子）必须严格按照现有左再有右的顺序，
不允许
1.没有左孩子节点但是有右孩子节点，例如：

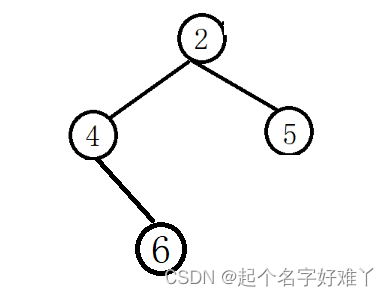
2.从上至下，按层往下，除了最后一层，其他层未达到最大节点数，例如：

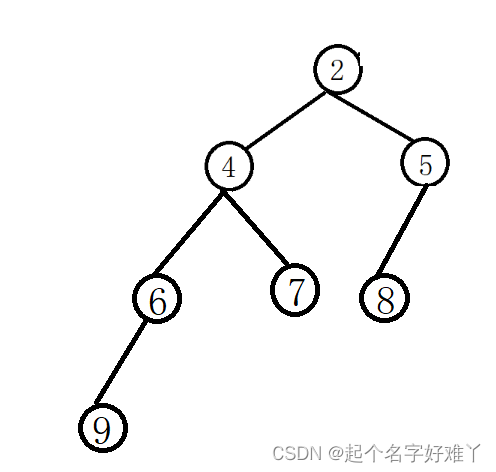
总结：
满二叉树 从上到下，从左至右，从 0 ~ n 中间 不间断
完全二叉树：每一层(根节点为第 0 层)的节点数都满足 2^n 个

二、顺序存储构建二叉树

例如：给定一个vector 包含若干个元素，要求按照元素的顺序构建出一颗二叉树

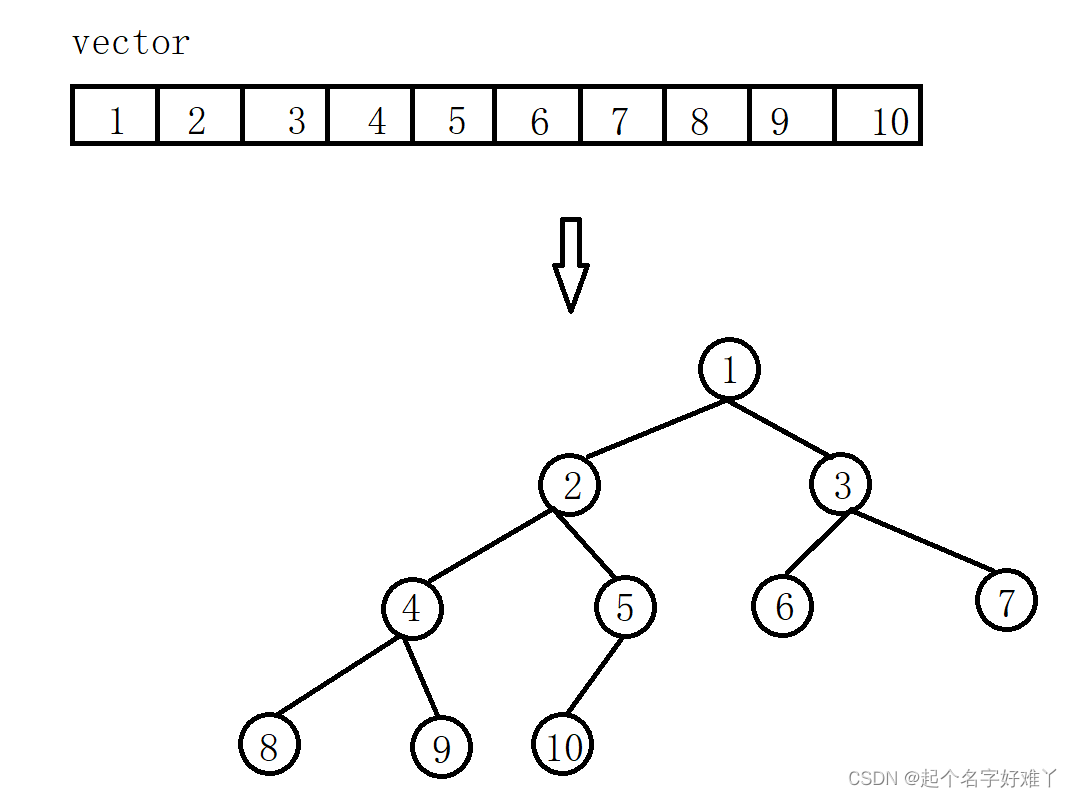
刚开始可能没有思路，那我们先看一下二叉树的特点

1.需要存储当前节点的值
2.通过该节点可以找到左孩子、右孩子

通过上述两个特点，我们可以想象出二叉树每个节点的大概结构

1.data 存储节点的值
2.left 指针 ，访问该节点的左孩子节点
3.right 指针，访问该节点的右孩子节点

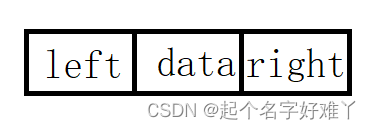
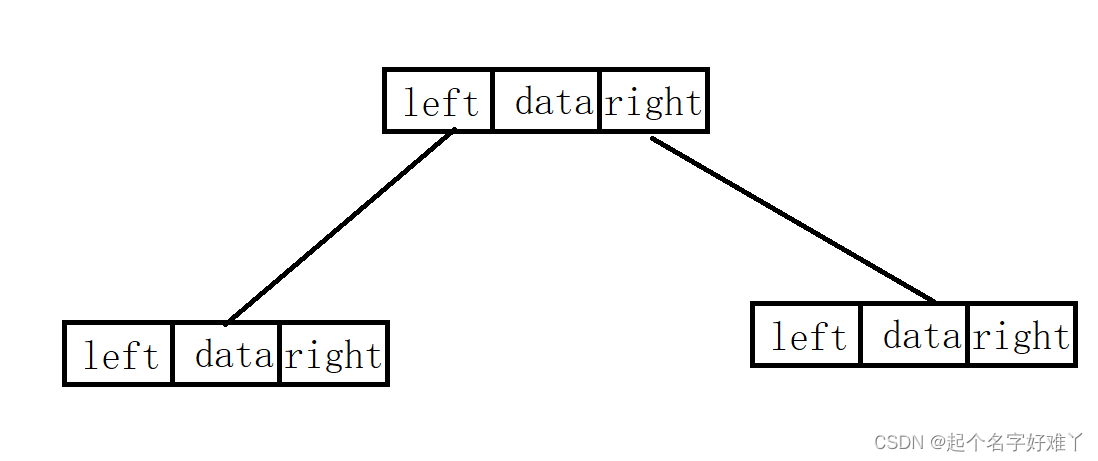
代码则为：

struct TreeNode
{int val;TreeNode* left;TreeNode* right;
};

二叉树的节点类型确定了，那么我们如何将数组中的元素，构建成一个逻辑上的树形结构呢？
我们来分析一下数组元素下标与构建成功之后的二叉树的下标关系

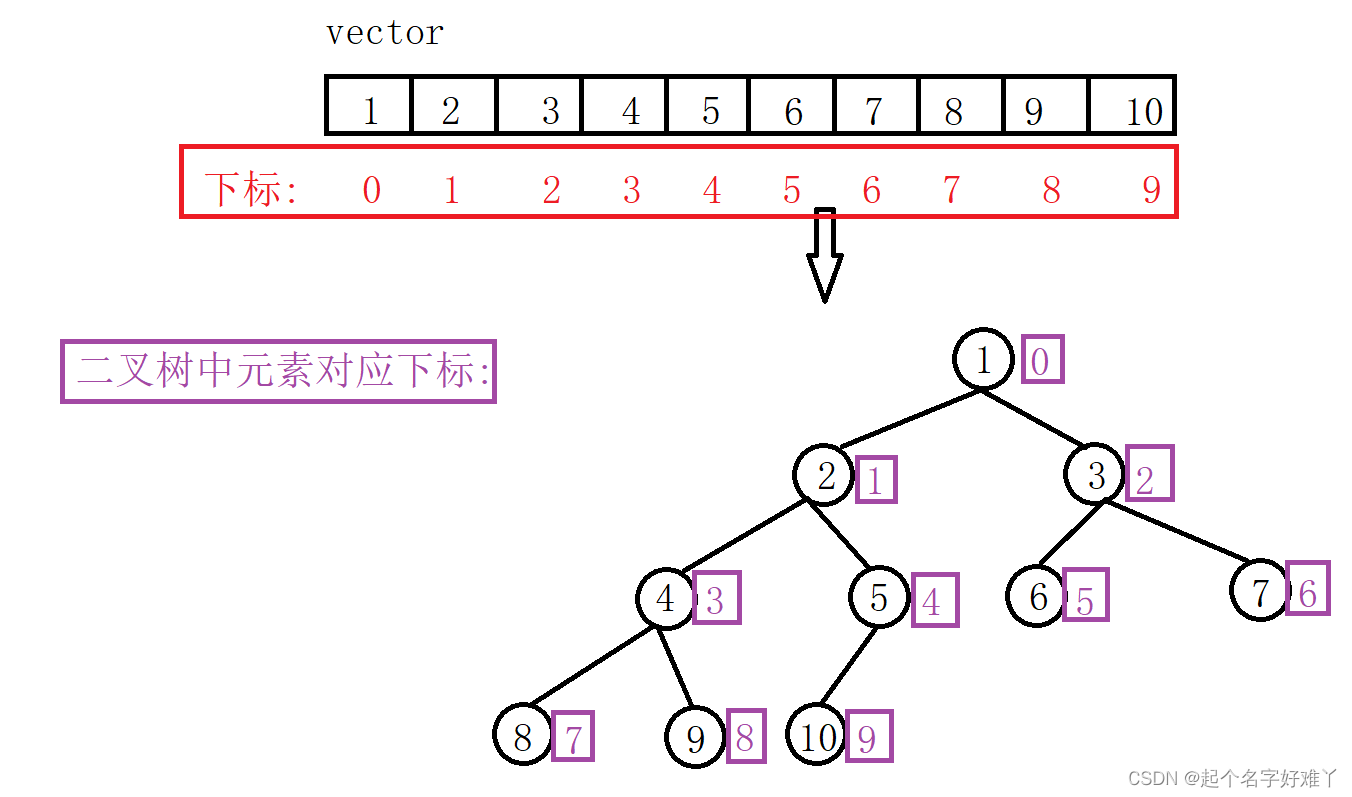
通过分析二叉树中元素下标我们可以总结一下规律：
设 当前节点的元素下标为 n ，那么该节点的左孩子 节点元素下标为 2n + 1,右孩子节点元素下标为 2n+2;
例如：

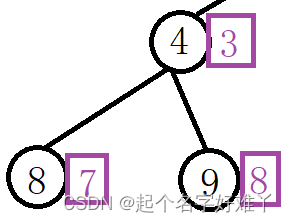
现在将节点和数组元素的关系理清之后，接下来需要考虑如何将数组中的元素逐个，按照二叉树中从上至下，从左至右构建。

这里我们需要用到队列来控制从上至下、从左至右顺序；
通过入队(根、左、右)、取队头、出队，保持顺序，通过元素下标控制节点的值

	TreeNode* MakeBinaryTree(vector& vctTemp){if (vctTemp.empty()){cout << "vector is empty" << endl;return nullptr;}else{//先将根节点入队TreeNode* root = new TreeNode();root->val = vctTemp[0];root->left = nullptr;root->right = nullptr;queue quTemp;quTemp.push(root);//元素下标int n = 0;while (!quTemp.empty()){	//先取出队头元素TreeNode* nodeTemp = quTemp.front();quTemp.pop();//计算左孩子节点下标int leftIndex = 2 * n + 1;if (leftIndex <= vctTemp.size() - 1){//构建左孩子节点TreeNode* leftnode = new TreeNode();leftnode->val = vctTemp[leftIndex];leftnode->left = nullptr;leftnode->right = nullptr;nodeTemp->left = leftnode;quTemp.push(leftnode);}//计算右孩子节点下标int rightIndex = 2 * n + 2;if (rightIndex <= vctTemp.size() - 1){//构建右孩子节点TreeNode* rightnode = new TreeNode();rightnode->val = vctTemp[rightIndex];rightnode->left = nullptr;rightnode->right = nullptr;nodeTemp->right = rightnode;quTemp.push(rightnode);}//下标 + 1,每次仅出队一个元素n++;}return root;}}

三、常规遍历方法

3.1 广度优先遍历

广度优先遍历 英文简称为：BFS (Breadth-First-Search)

广度优先从上至下，从左至右依次进行遍历，这里是不是想到了我们构建的时候也是按照从上至下，从左至右的构建顺序，没错这种方法就是 BFS 广度优先遍历
按照构建的思路，我们同样需要一个队列来辅助我们进行顺序控制

图示：


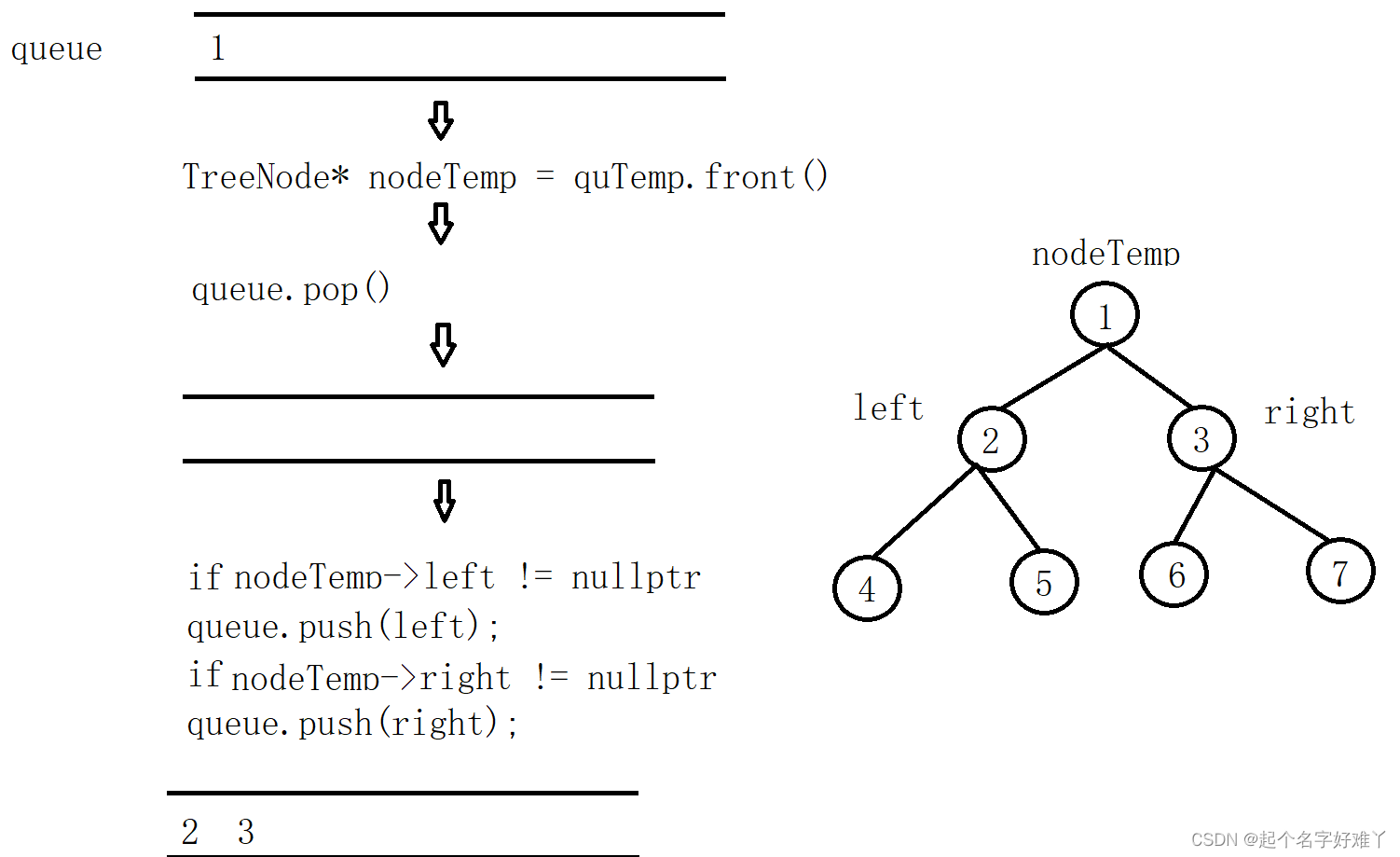
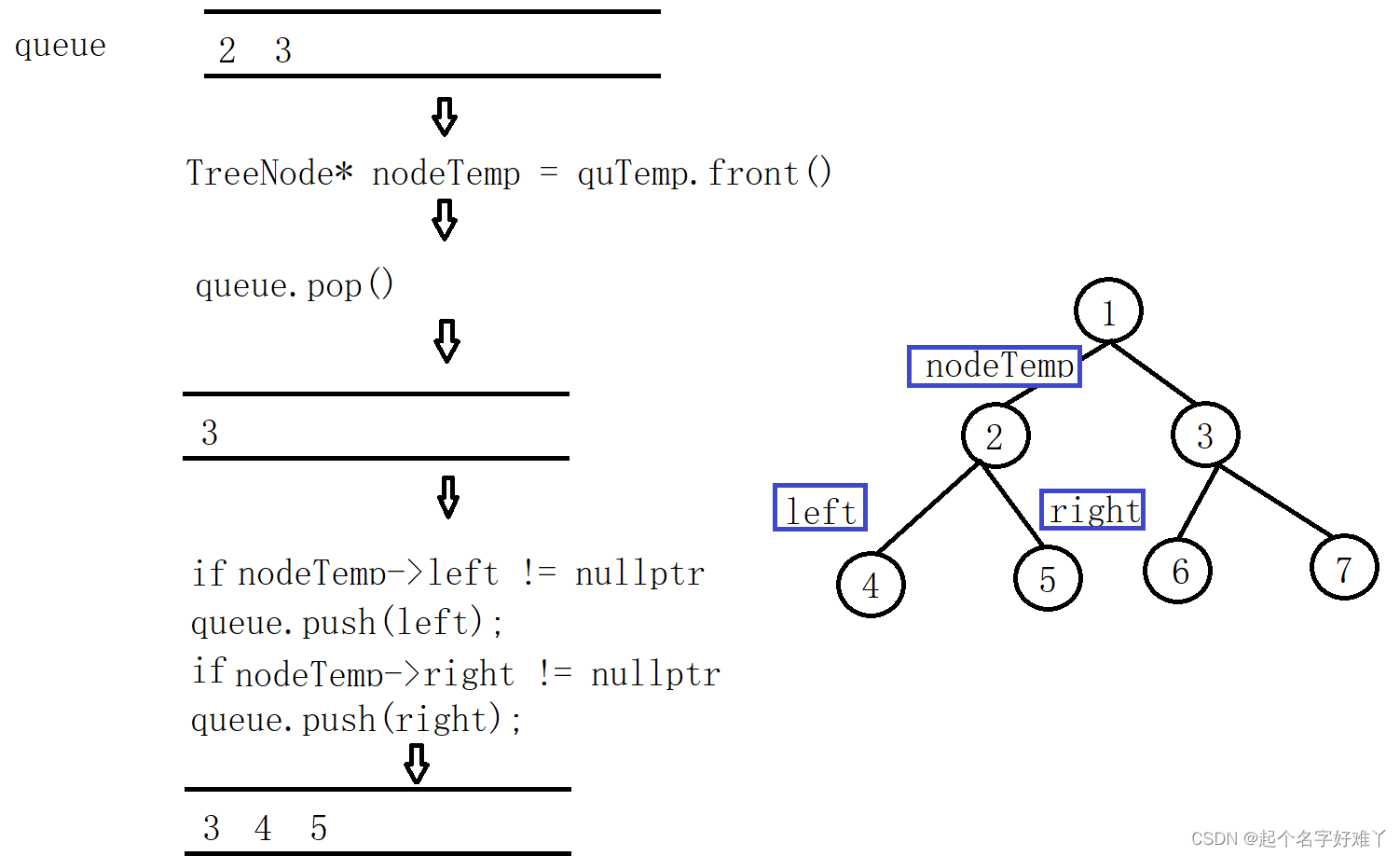
直到最后一个叶子节点 7 pop 出去，queue 为空循环结束，整个二叉树也遍历完成

代码示例：

	void BFS(TreeNode* root){if (root == nullptr){cout << " root is empty" << endl;}else{vector vctResult;queue quTemp;//先将根节点入队quTemp.push(root);vctResult.push_back(root->val);while (!quTemp.empty()){//取队头TreeNode* nodeTemp = quTemp.front();quTemp.pop();//左孩子不为空，先将左孩子入队if (nodeTemp->left != nullptr){quTemp.push(nodeTemp->left);vctResult.push_back(nodeTemp->left->val);}//右孩子不为空，再将右孩子入队if (nodeTemp->right != nullptr){quTemp.push(nodeTemp->right);vctResult.push_back(nodeTemp->right->val);}}//打印元素Print(vctResult);}}

运行：

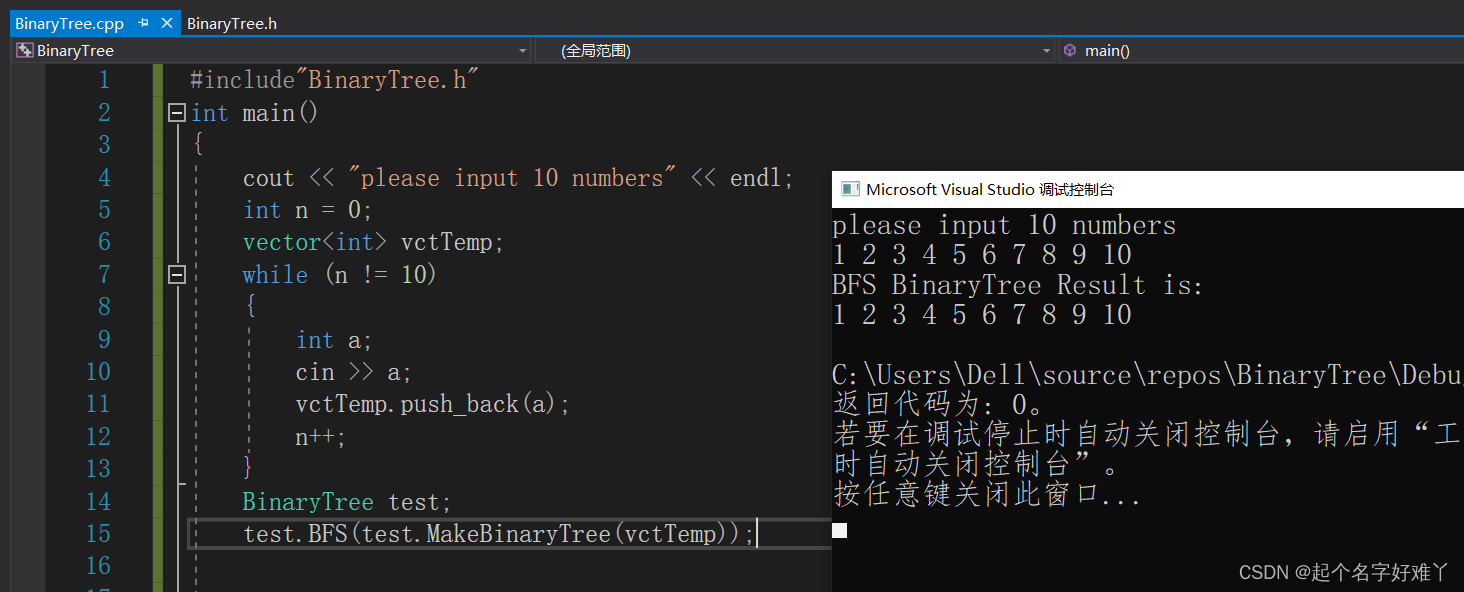
3.2 深度优先遍历

深度优先遍历不同于广度优先那样一层一层、从左至右遍历，而是按照前序或中序、或后序那样，从根节点不断的向下遍历，并将整棵树分左右子树，先将一颗子树遍历完（达到该子树的叶子节点)再去遍历另一棵树，因此被称为深度优先遍历。
深度优先遍历顺序又分为一下三种遍历方法：

以下是我整理的一篇二叉树的 前/中/后序 逻辑图形示例，不清楚逻辑的可以先看一下：
二叉树的前序/中序/后序遍历新手入门介绍

图示：

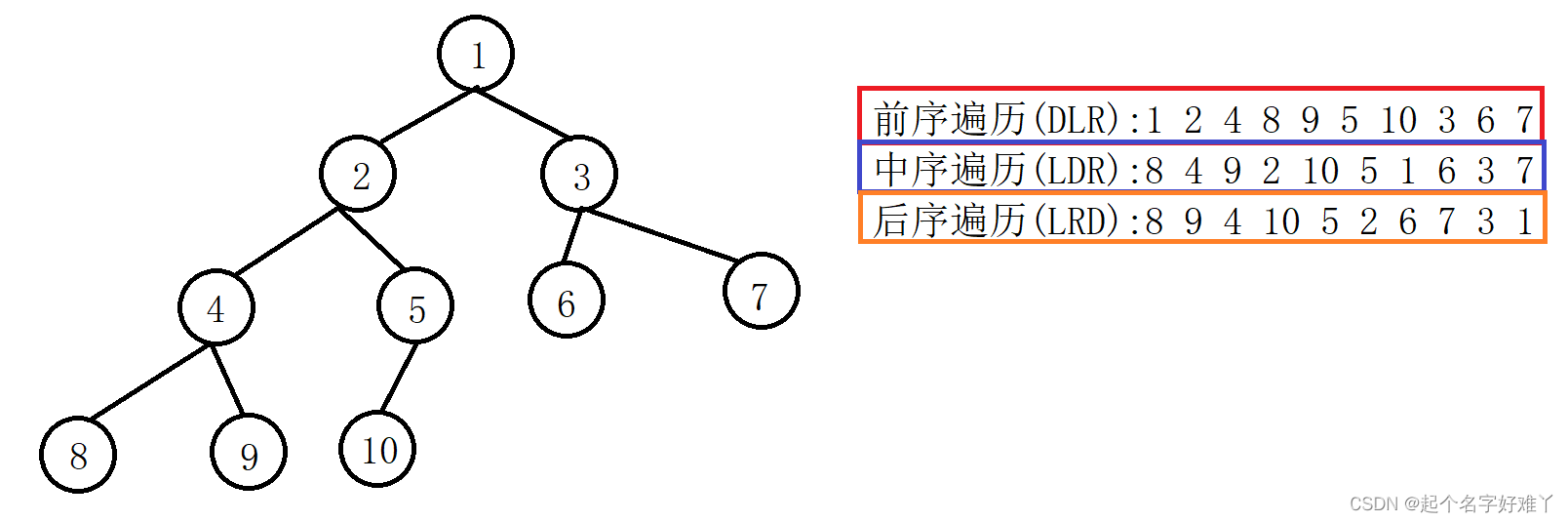
3.2.1前序遍历

前序遍历：遍历顺序(先根、再左、再右) DLR

递归遍历代码为：

	void DLR(TreeNode* root){if (root == nullptr){return;}cout << root->val << " ";DLR(root->left);DLR(root->right);}

关于递归的思想我们这里以前序遍历做详细的步骤分析，帮助大家理解递归的思路和思想

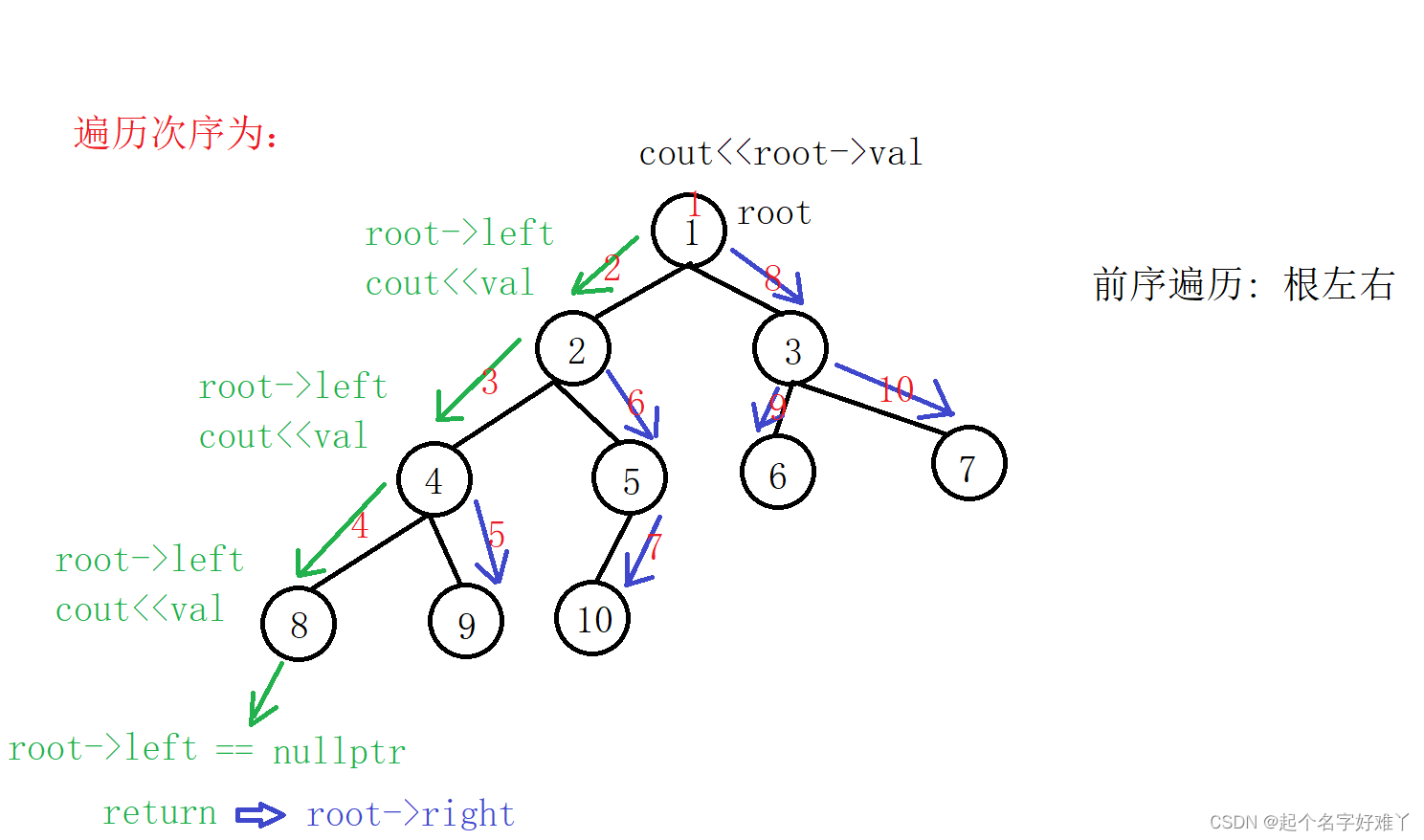
关于递归，大家可以有时候想不到递归函数如何去写，可以考虑以下三个方面，来思考递归怎么写

1.函数调用自身
2.函数终止条件
3.向终止条件前进的执行动作

例如：

	//递归函数本身void DLR(TreeNode* root){//终止条件if (root == nullptr){return;}cout << root->val << " ";//不断向叶子节点遍历，逼近 root == nullptr 条件//调用函数自身DLR(root->left);DLR(root->right);}

3.2.2 中序遍历

中序遍历：遍历顺序(先左、再根、再右)
递归遍历代码为：

	void LDR(TreeNode* root){if (root == nullptr){return;}LDR(root->left);cout << root->val << " ";LDR(root->right);}

3.2.3后序遍历

后序遍历：遍历顺序(先左、再右、再根)
递归遍历代码为：

	//后序遍历void LRD(TreeNode* root){if (root == nullptr){return;}LRD(root->left);LRD(root->right);cout << root->val << " ";}

完整测试代码如下：
BinaryTree.h

#pragma once
#include
#include
#include
using namespace std;struct TreeNode
{int val;TreeNode* left;TreeNode* right;
};class BinaryTree
{
public:BinaryTree(){}~BinaryTree(){}TreeNode* MakeBinaryTree(vector& vctTemp){if (vctTemp.empty()){cout << "vector is empty" << endl;return nullptr;}else{TreeNode* root = new TreeNode();root->val = vctTemp[0];root->left = nullptr;root->right = nullptr;queue quTemp;quTemp.push(root);int n = 0;while (!quTemp.empty()){TreeNode* nodeTemp = quTemp.front();quTemp.pop();int leftIndex = 2 * n + 1;if (leftIndex <= vctTemp.size() - 1){TreeNode* leftnode = new TreeNode();leftnode->val = vctTemp[leftIndex];leftnode->left = nullptr;leftnode->right = nullptr;nodeTemp->left = leftnode;quTemp.push(leftnode);}int rightIndex = 2 * n + 2;if (rightIndex <= vctTemp.size() - 1){TreeNode* rightnode = new TreeNode();rightnode->val = vctTemp[rightIndex];rightnode->left = nullptr;rightnode->right = nullptr;nodeTemp->right = rightnode;quTemp.push(rightnode);}n++;}return root;}}void BFS(TreeNode* root){if (root == nullptr){cout << " root is empty" << endl;}else{vector vctResult;queue quTemp;quTemp.push(root);vctResult.push_back(root->val);while (!quTemp.empty()){TreeNode* nodeTemp = quTemp.front();quTemp.pop();if (nodeTemp->left != nullptr){quTemp.push(nodeTemp->left);vctResult.push_back(nodeTemp->left->val);}if (nodeTemp->right != nullptr){quTemp.push(nodeTemp->right);vctResult.push_back(nodeTemp->right->val);}}cout << "BFS BinaryTree Result is:" << endl;Print(vctResult);}}//前序遍历void DLR(TreeNode* root){if (root == nullptr){return;}cout << root->val << " ";DLR(root->left);DLR(root->right);}//中序遍历void LDR(TreeNode* root){if (root == nullptr){return;}LDR(root->left);cout << root->val << " ";LDR(root->right);}//后序遍历void LRD(TreeNode* root){if (root == nullptr){return;}LRD(root->left);LRD(root->right);cout << root->val << " ";}void Print(vector &vctTemp){for (auto a : vctTemp){cout << a << " ";a++;}cout << endl;}
private:vector m_vector;};

BinaryTree.cpp

#include"BinaryTree.h"
int main()
{cout << "please input 10 numbers" << endl;int n = 0;vector vctTemp;while (n != 10){int a;cin >> a;vctTemp.push_back(a);n++;}BinaryTree test;TreeNode* root = test.MakeBinaryTree(vctTemp);test.BFS(root);cout << "前序遍历结果为:" << endl;test.DLR(root);cout << endl;cout << "中序遍历结果为:" << endl;test.LDR(root);cout << endl;cout << "后序遍历结果为:" << endl;test.LRD(root);cout << endl;return 0;
}