软件设计师笔记-----数据结构与算法基础
六、数据结构与算法基础
6.1、数组与矩阵
6.1.1、概述
数组下标的转化问题
稀疏矩阵
上三角
下三角等类型的矩阵
6.1.2、数组

存储地址的计算问题,以及在二维数组当中按行存储和按列存储的区别
主要是去了解 按行 和 按列 进行存储的时候 地址的计算问题
6.1.3、稀疏矩阵
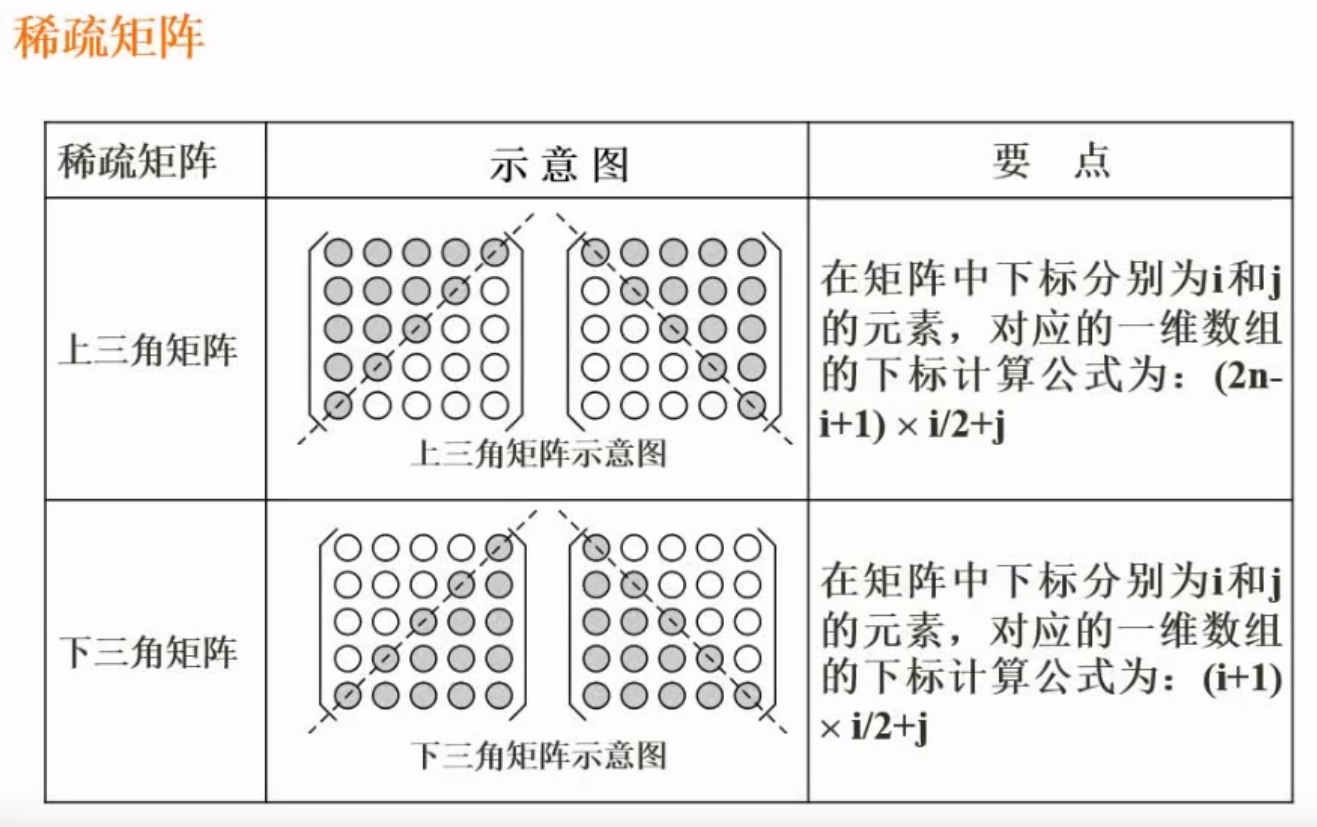
上三角公式 :
i(2n−i+1)2+j\frac {i (2n - i + 1)} {2} + j 2i(2n−i+1)+j
下三角公式:
i(i+1)2+j\frac {i (i + 1)} {2} + j 2i(i+1)+j
使用带入法,先把 A0,0带入,得到相应的M1 ,就可以排除 B和C了 因为BC是得到的M0, 然后在带入一个数进行对AD的排除之后得出结果
数据结构的定义
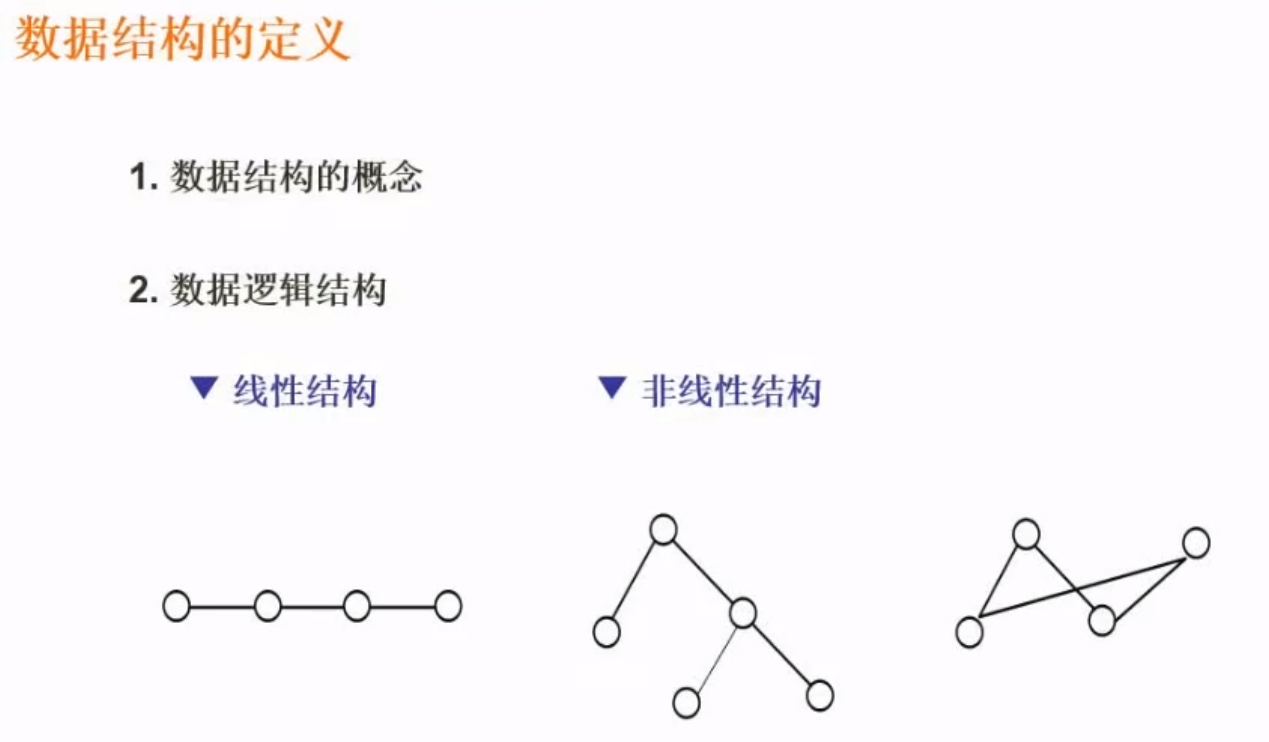
数据逻辑结构
- 线性结构
- 非线性结构
6.2、线性表
栈和队列基本特性与相关的应用,几乎每次都考
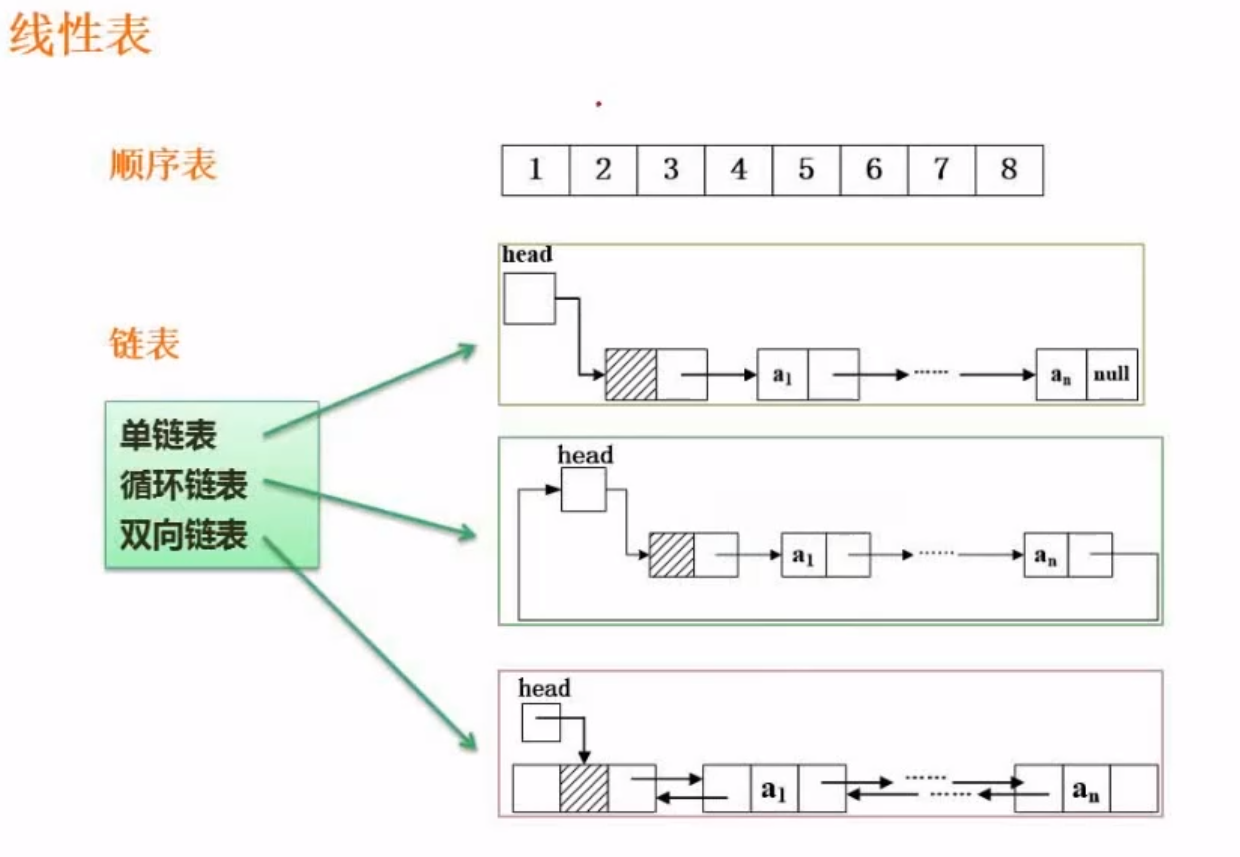
顺序表和链表
顺序表
- 连续
链表
- 不连续
- 链表里面存的有下一个元素的指针
- 分类
- 单链表
- 循环链表
- 双向链表
链表的操作
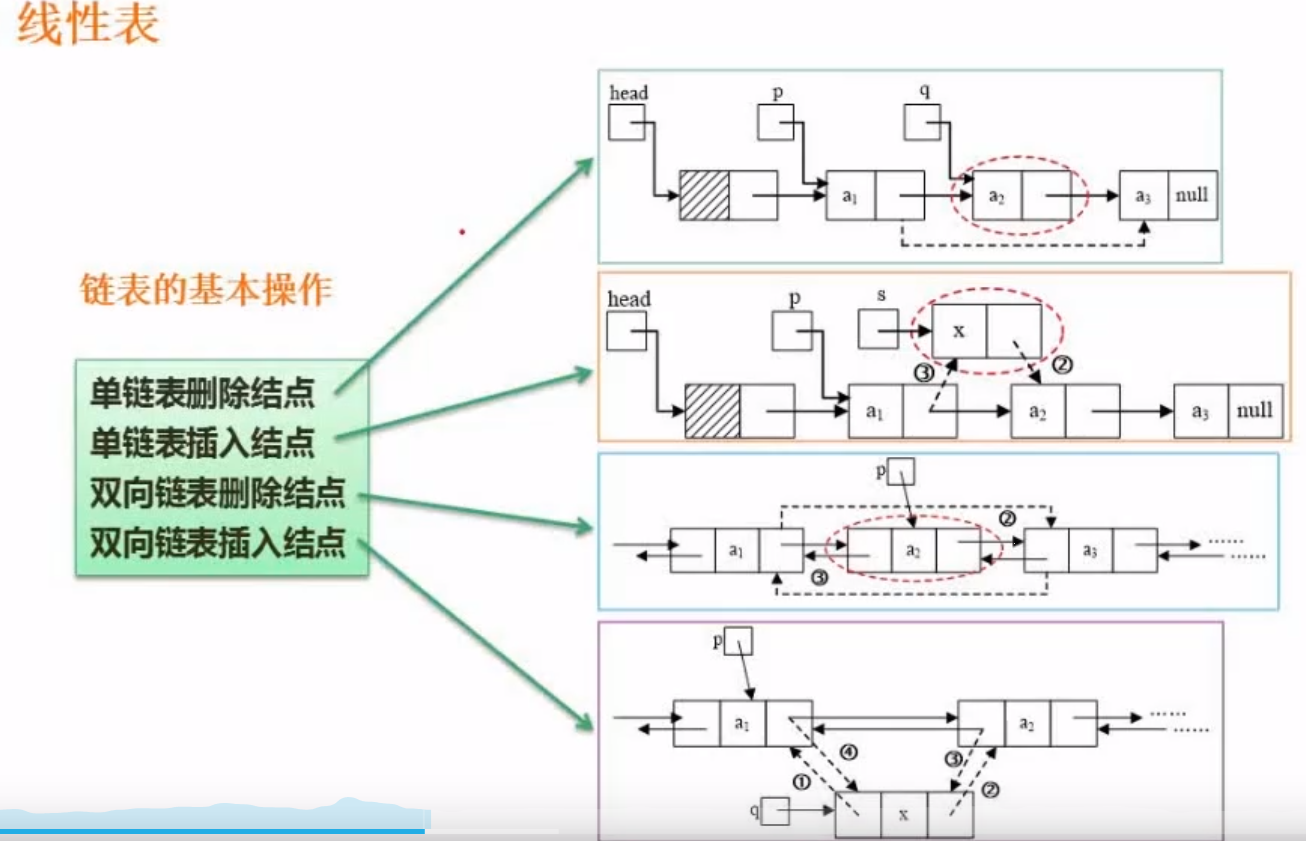
单链表删除结点:
- p的next 指针 = q 的next 指针
单链表插入结点:
- s的next = p 的next
- p的next= s
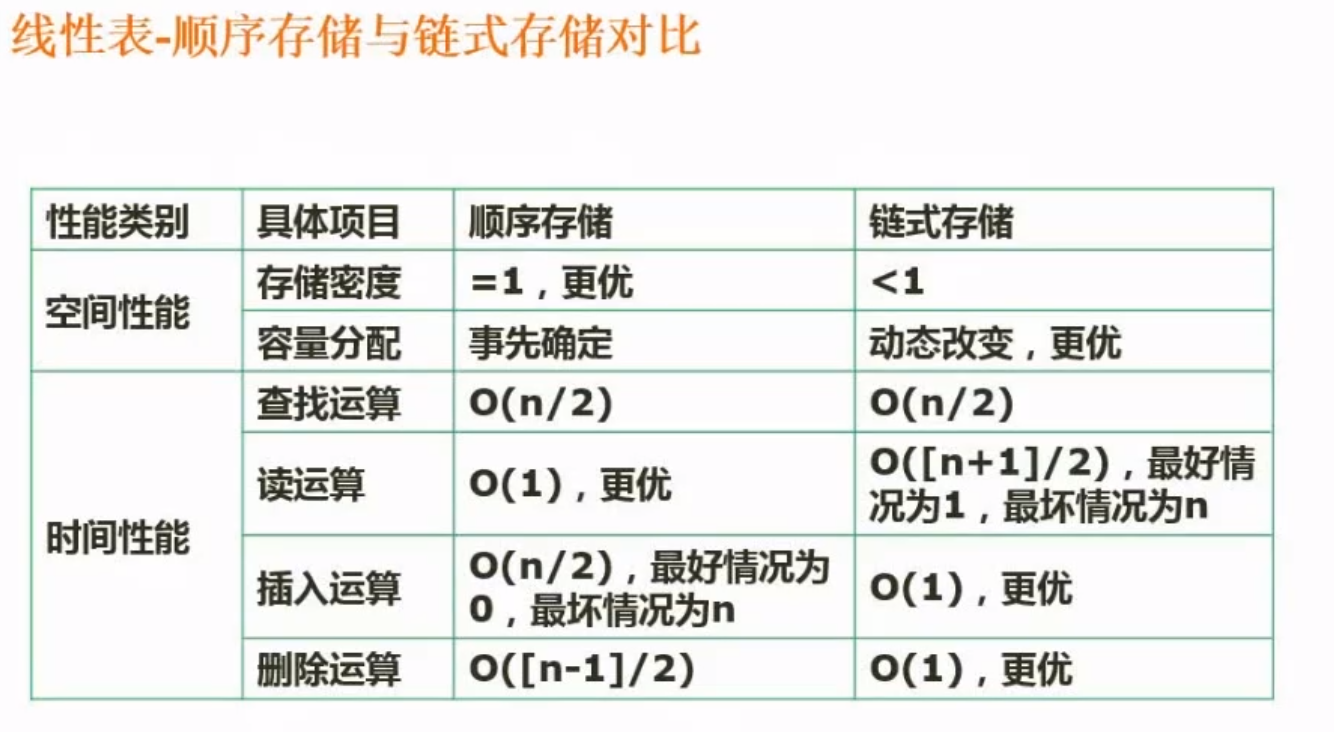
顺序存储和链式存储的对比
队列和栈
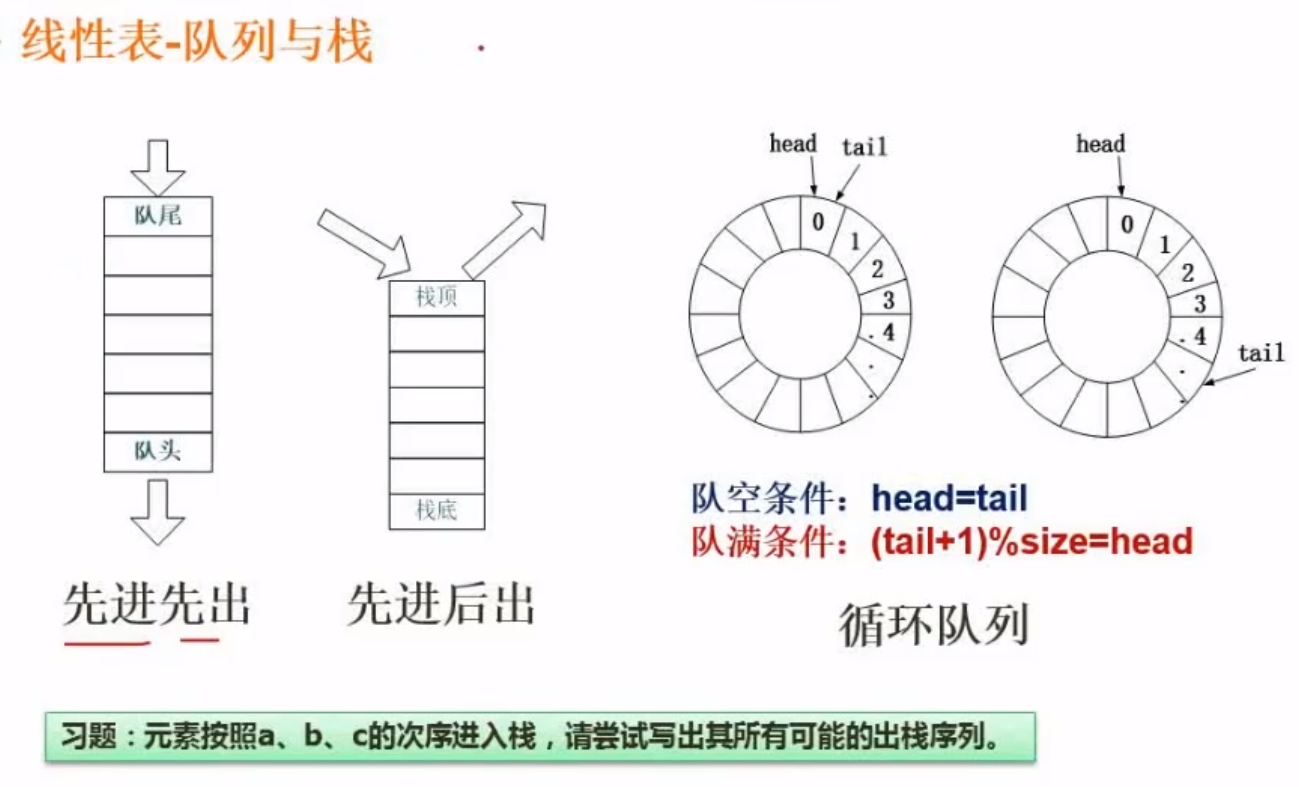
队列:
- 先进先出
Z栈:
- 先进后出
循环队列
- 当队空的时候是 队头=队尾
- 队尾总是指向最后一个元素的下一个位置
- 所以当队存满的时候队尾同样指向了队头,这这样就产生了麻烦,所以解决 方案就是,循环队列少存一个元素这样的话当队尾的下一个元素是队头的时候,就说明队满了, 用公式就是 (tail+1)%size = head 队尾+1 与队列的长度进行区域结果等于0则说明队满
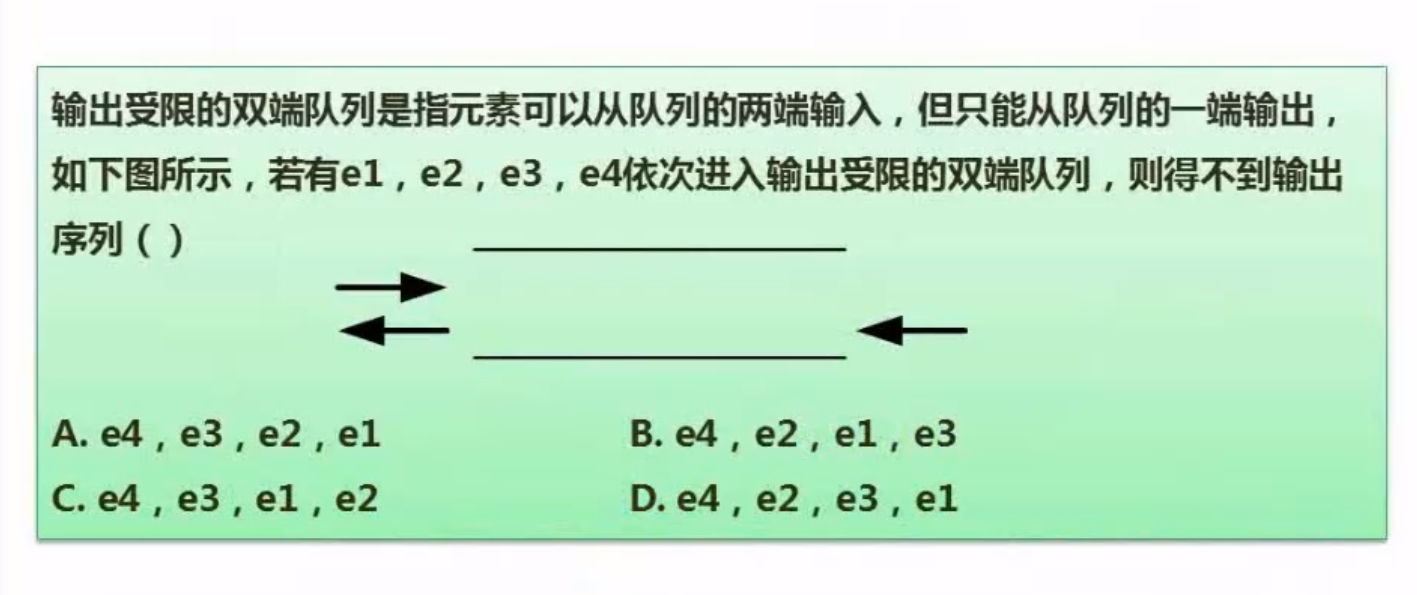
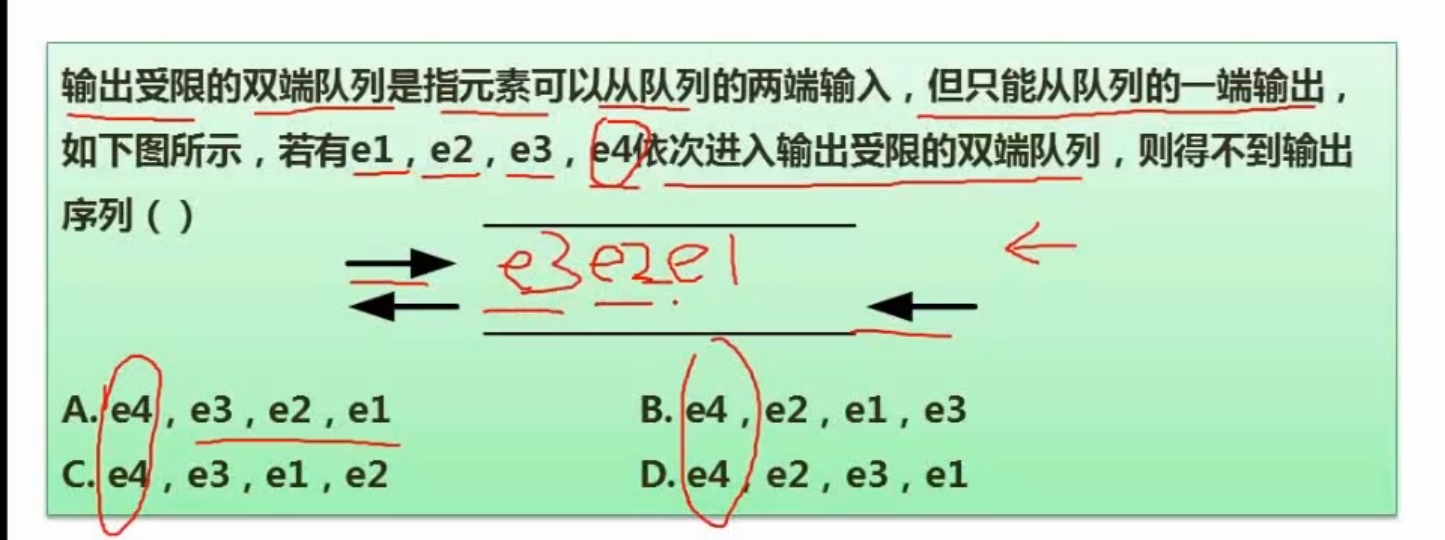
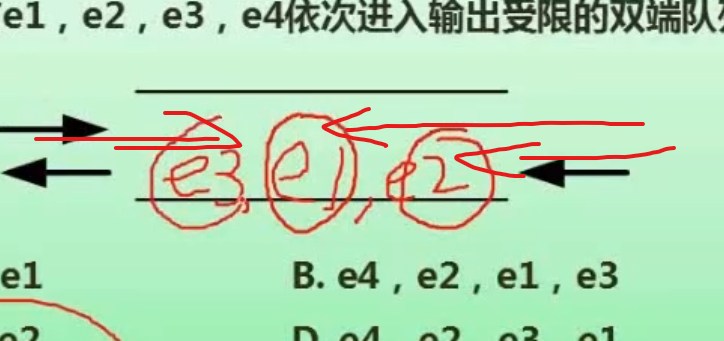
例题
解析:
A
B
C
D 无法实现,所以选D
答案选D
6.3、广义表
了解基本的概念和操作

基本操作
表头
- head(LS1) = 第一个元素
- tail(LS1) = 除了第一个元素之外 的剩余元素
6.4、数和二叉树
数和二叉树的基本特性,用这种数据结构一般用来解决什么样的问题,以及有特点有特色的二叉树他的基本情况
6.4.1、树
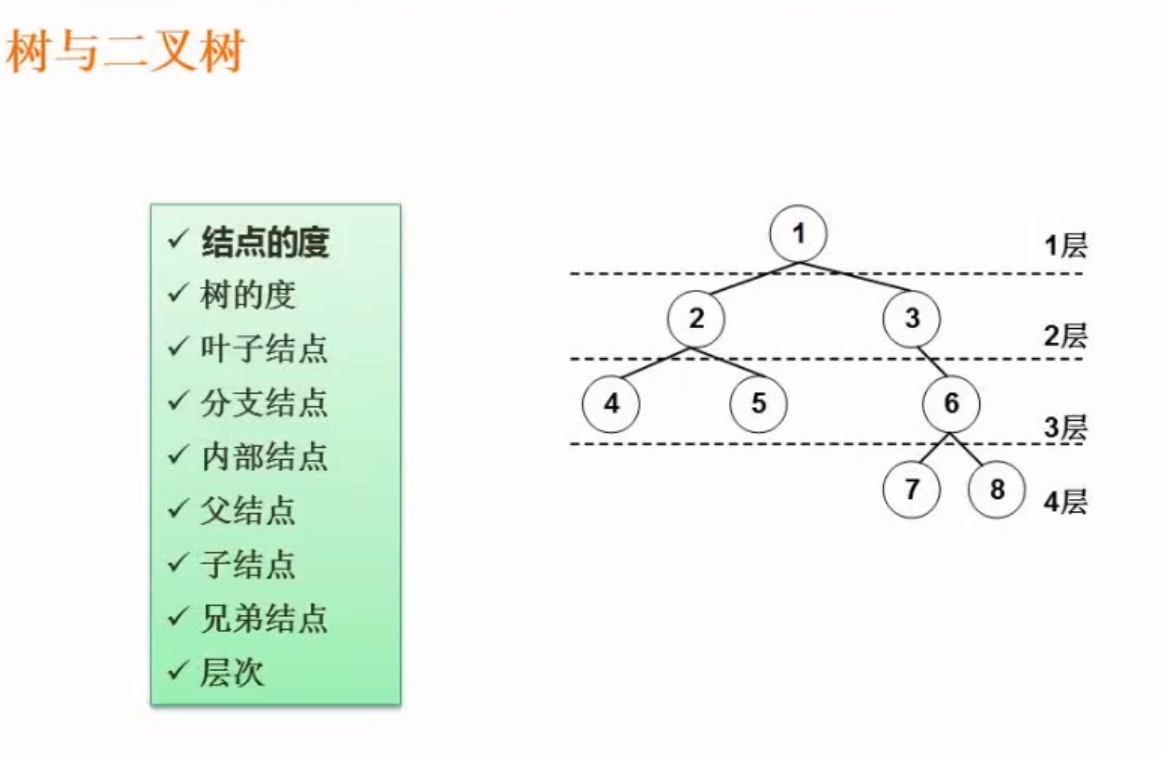
- 结点的度: 结点所拥有的的直接子结点数
- 例如 1的度为2 3的度为1 7的节点是0
- 树的度:所有结点当中度数最高的那个度
- 上图这个树的度为 2
- 叶子结点: 没有孩子节点的结点都是叶子结点
- 分支结点: 度不为0的结点;
- 内部结点: 即非根结点也非叶子结点的节点
- 父结点和子结点: 一个相对的概念
- 兄弟结点
- 层次
6.4.2、二叉树
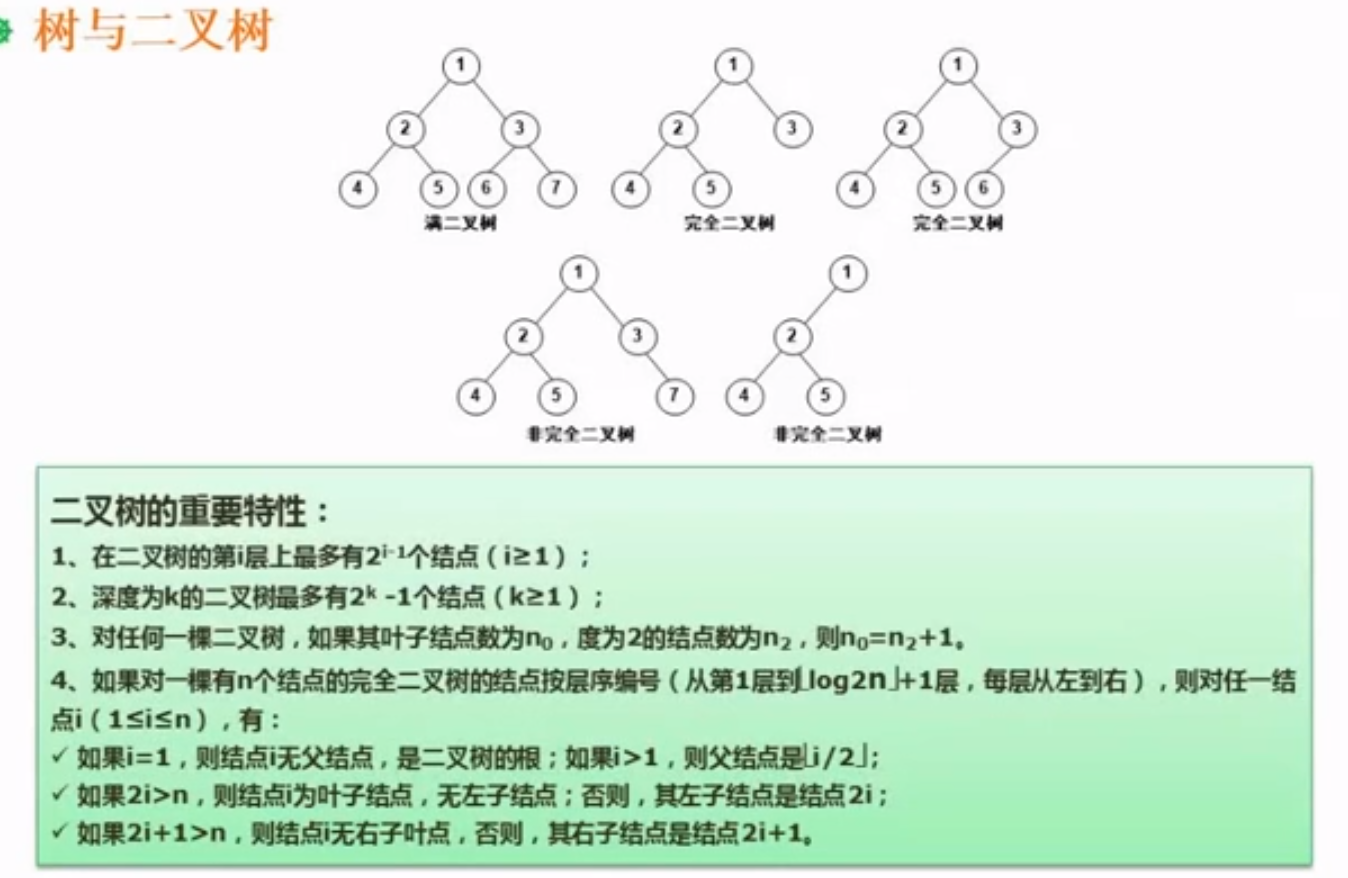
- 满二叉树
- 树没有缺失的结点
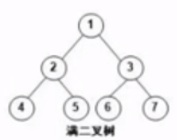
- 完全二叉树
- 除了最后一层其他都是满的,最后一层从左到右排列,左边的是满的右边是缺的
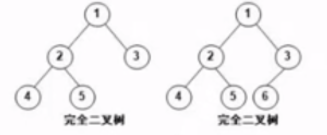
6.4.3、二叉树的重要特性
- 在二叉树的第i上最多有2i-1个结点(i>=1)
- 深度为k的二又树最多有2k-1个结点(k>=1)
- 对任何一棵二叉树,如果其叶子结点数为no,度为2的结点数为n2,则no=n2+1
- 如果对一棵有n个结点的完全二叉树的结点按层序号(从第1层到[log2n]+1层,每层从左到右),则对任一结
点i (1 ≤ i ≤ n),有:- 如果i=1,则结点无父结点,是二叉树的根;如果>1,则父结点是i/2
- 如果2i>n,则结点为叶子结点,无左子结点;否则,其左子结点是结点2i;
- 如果2+1>n,则结点无右子叶点,否则,右子结点是结点2i+1
6.4.4、二叉树的遍历
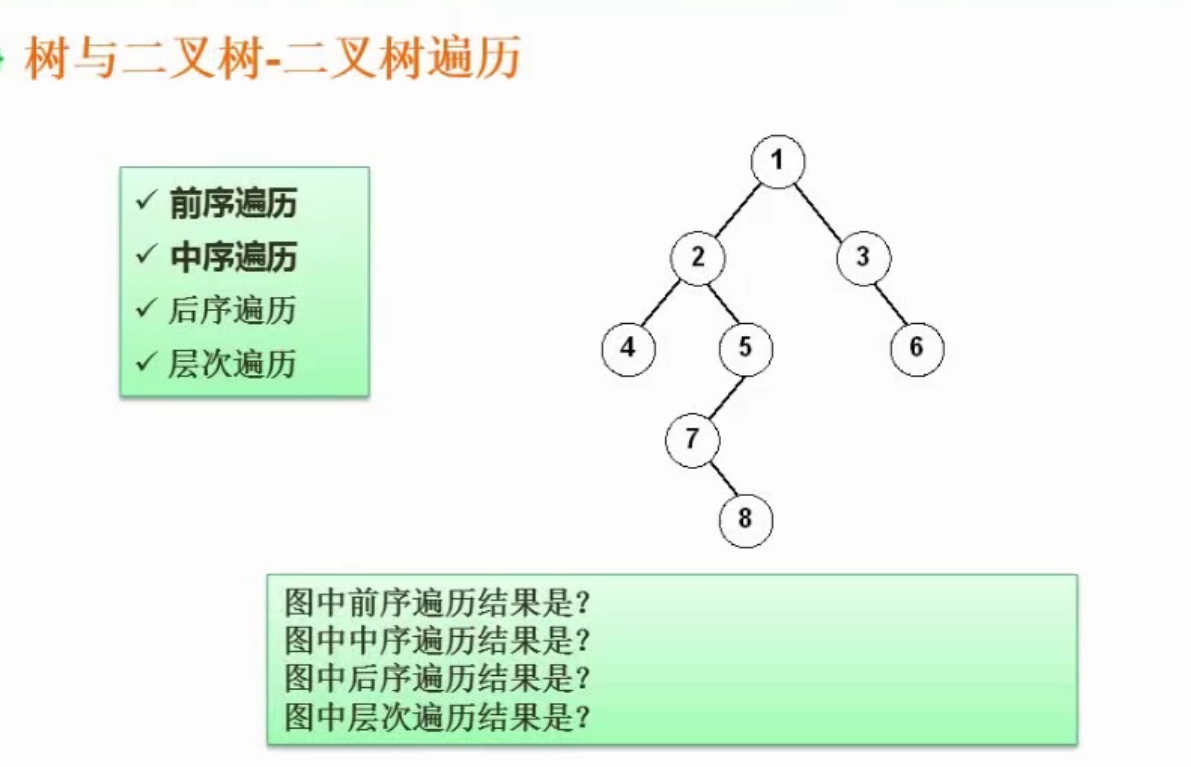
二叉树的遍历分为两组
第一组中的前中后是指的在什么时候访问根结点
-
第一组
- 前序遍历 根 → 左 → 右
- 先访问根结点在访问左子树和右子树结点
- 1 2 4 5 7 8 3 6
- 中序遍历 左→ 根→ 右
- 先访问左子树结点在访问根结点在访问右子树结点
- 4 2 7 8 5 1 3 6
- 后序遍历 左→ 右→ 根
- 先访问左子树结点在访问右子树结点在访问根结点
- 4 8 7 5 2 6 3 1
- 前序遍历 根 → 左 → 右
-
第二组
- 层次遍历
- 从第一层开始,从左到右从上到下依次遍历
- 上图所示: 1 2 3 4 5 6 7 8
- 层次遍历
6.4.5、反向构造二叉树
反向构造二叉树就是根据序列来还原二叉树
注意: 有前序和中或中序和后序 都可以将 一颗二叉树给还原出来 ,如果说仅仅有前序和后序我们不能够还原二叉树
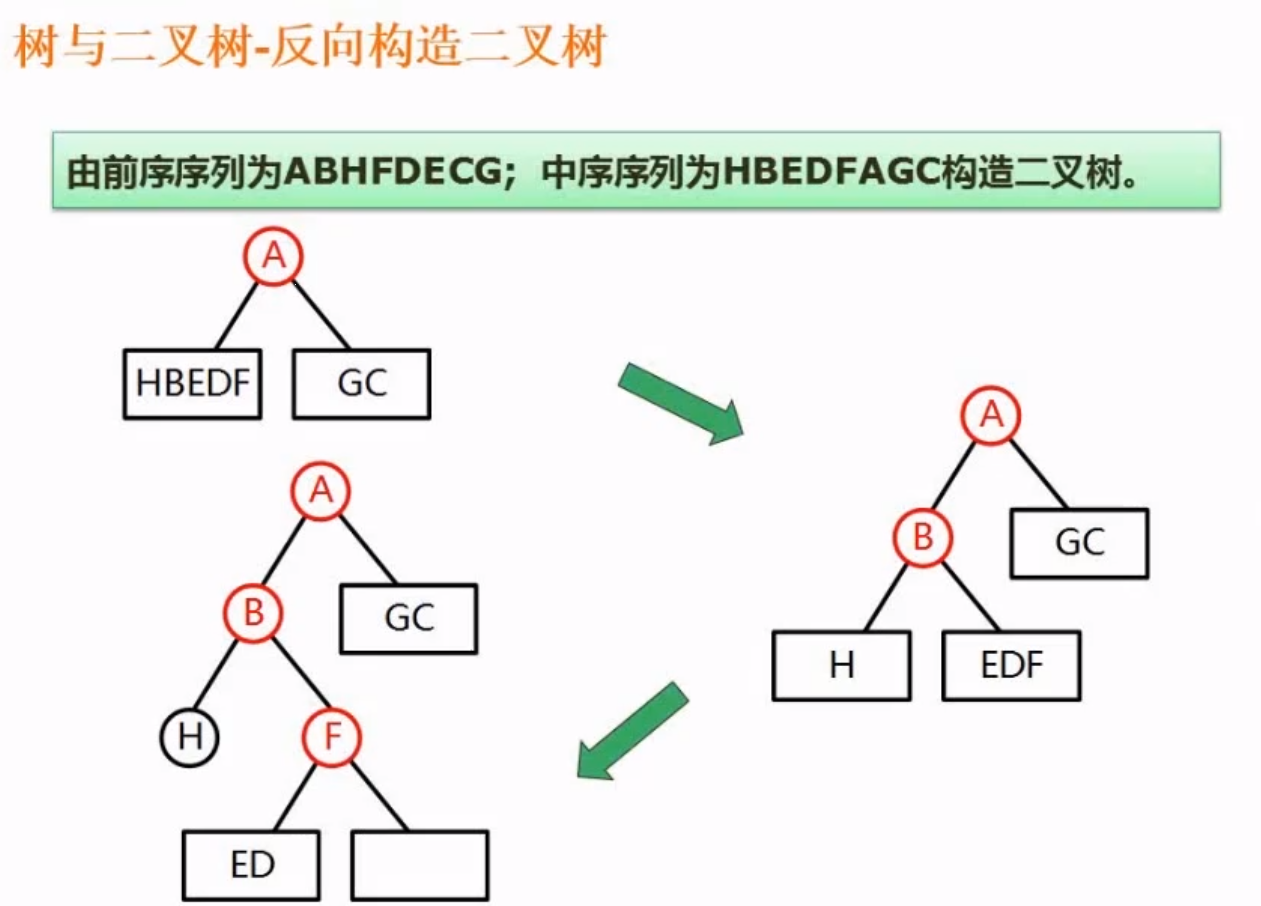
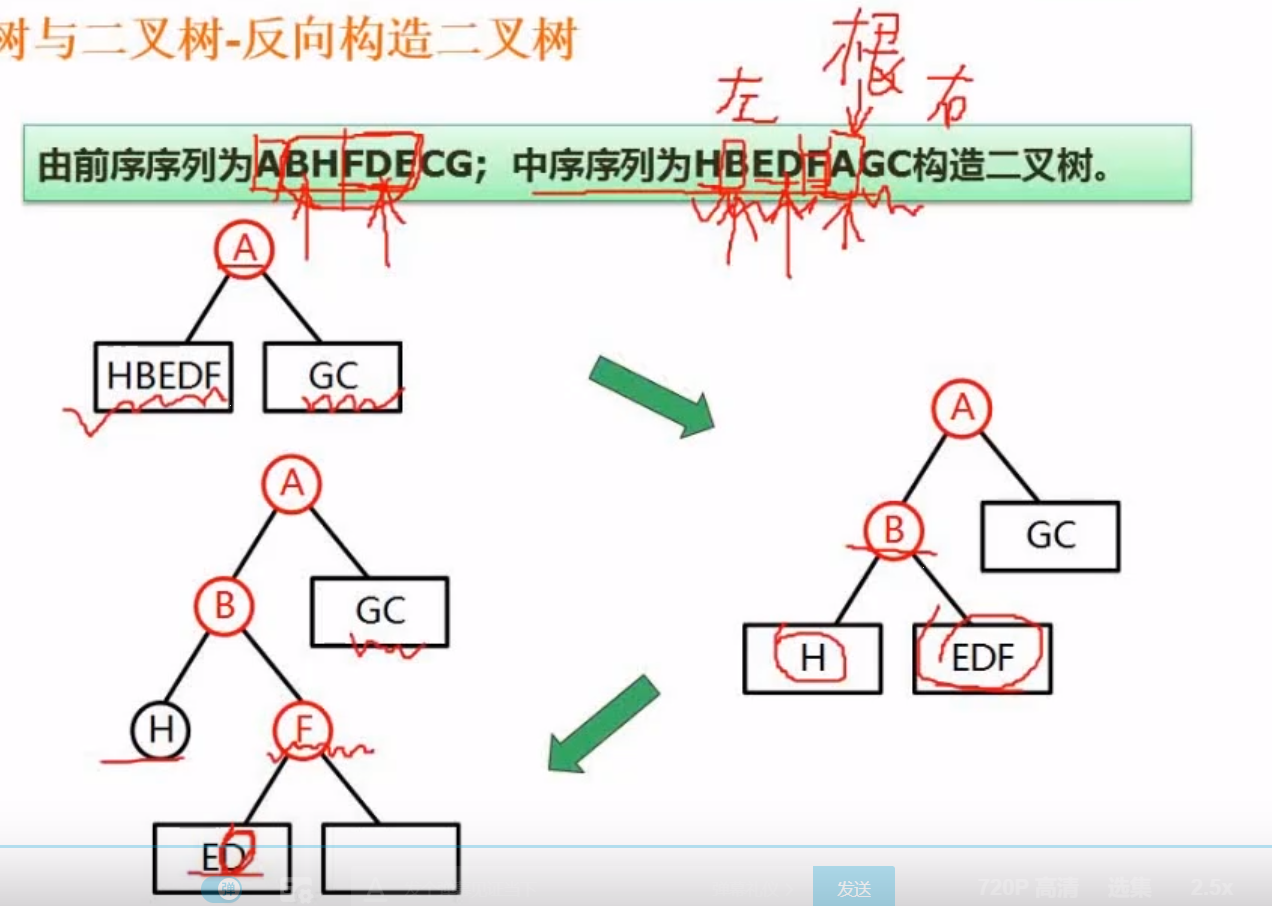
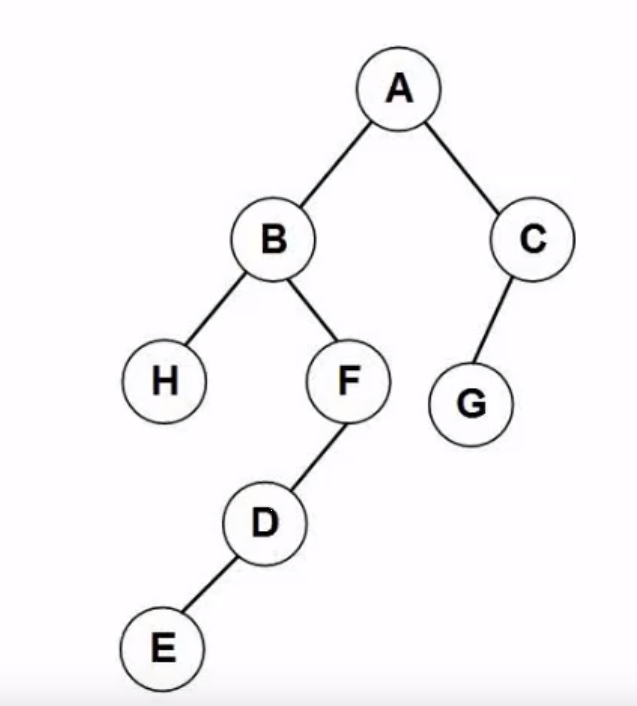
例题
思路如下: 先看前序序列 A是第一个说明A 就是根结点 ,然后在中序序列中找到A的位置,根据A的位置将二叉树分为左右两部分 BHFDE 和GC
然后继续看前序的BHFDE ,这里B是根结点,再去中序序列中查找,发现又可以分为 H 和FDE 两个 依次类推结果如下
6.4.6、树转二叉树
原则:
- 孩子结点
- 都会成为这棵树的左子节点
- 兄弟结点
- 都会成为这棵树的右子结点
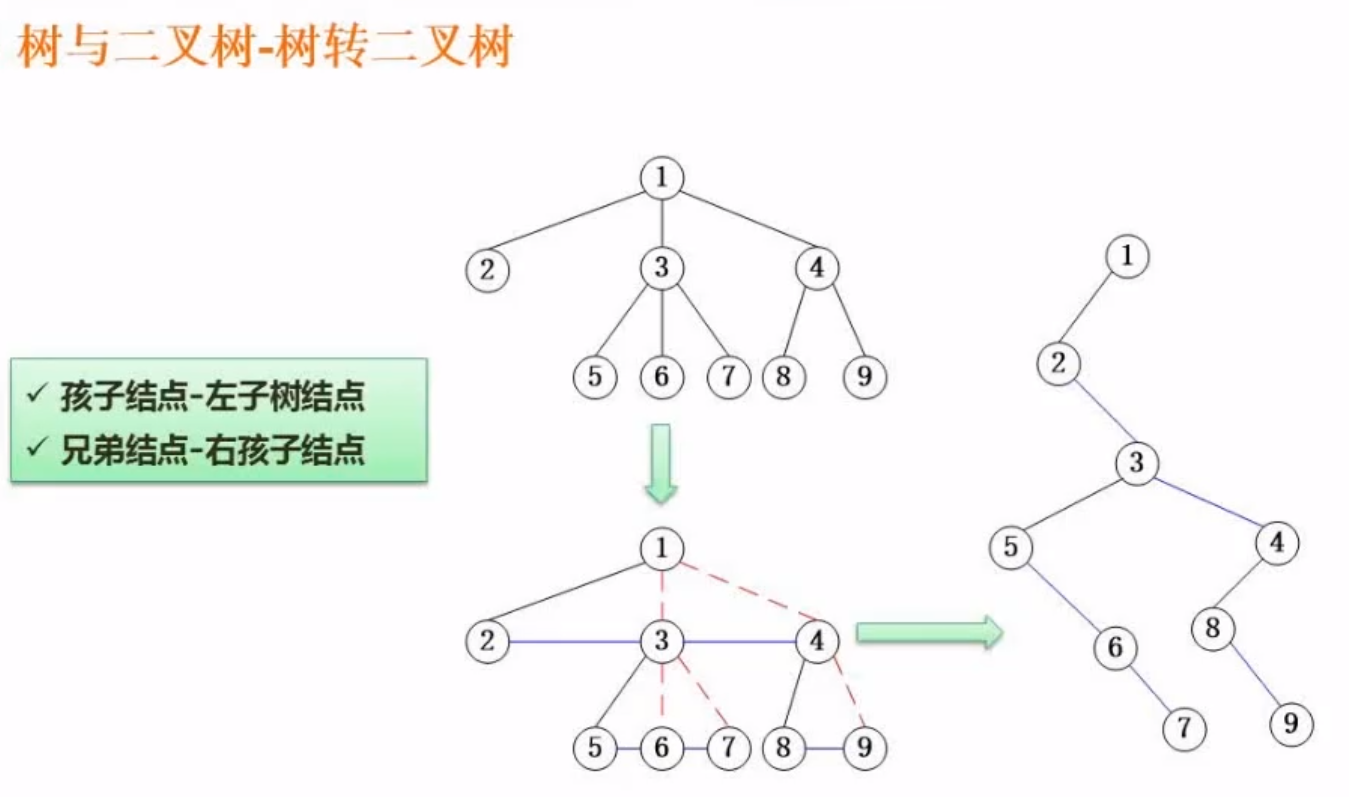
快速的方法是通过连线法:
连线法:孩子结点只保留最左边的线,兄弟结点通过 横线直接连起来,然后把多余的线擦除掉,旋转一下就行
例如: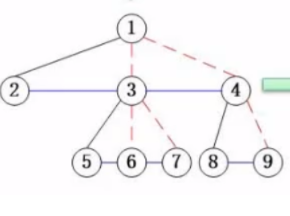
6.4.7、查找二叉树(又称排序二叉树)
特点:
- 查找二叉树的所有左子树结点都要比根结点要小
- 右子树结点都要比根结点要大
- 子树也满足上述条件
意义:
- 极大地提高查询的效率

6.4.8、最优二叉树(又称哈夫曼树)
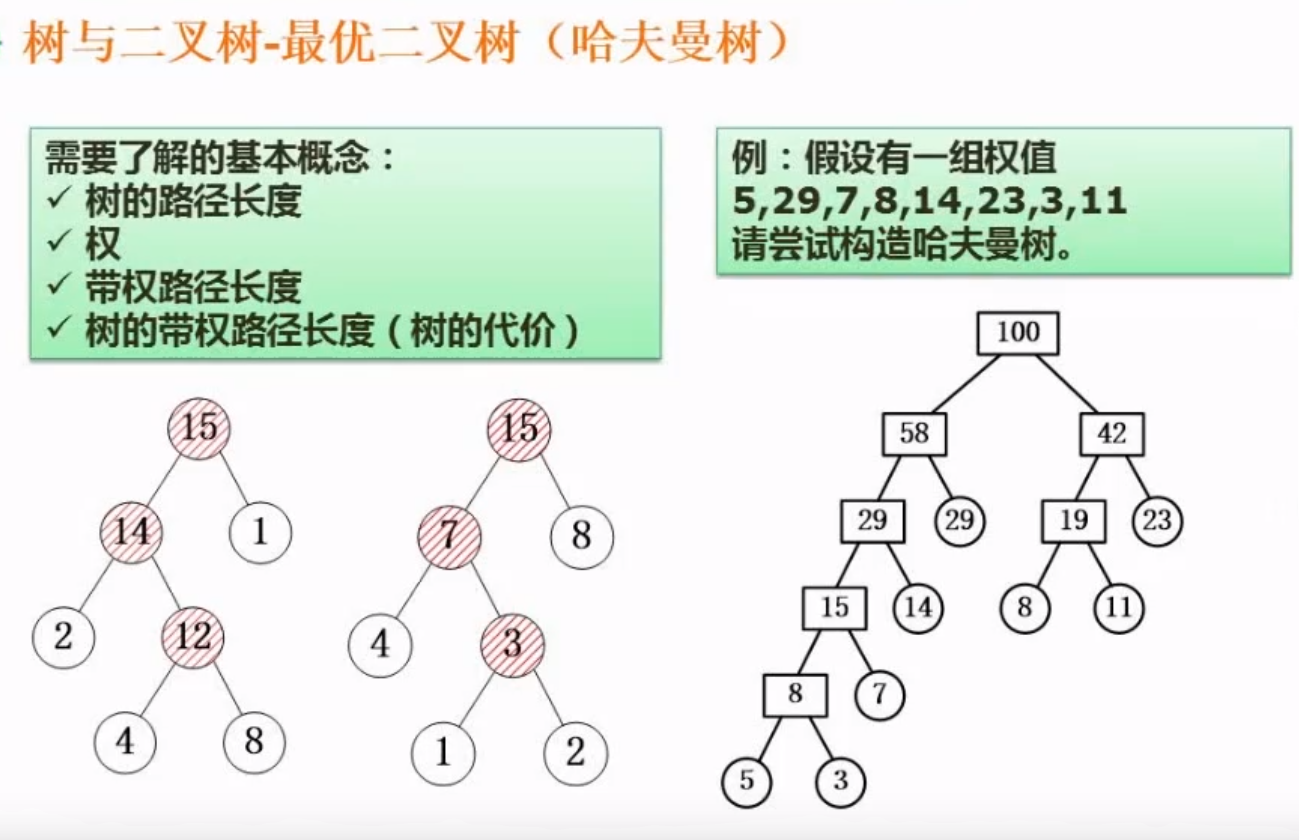
最优二叉树用于哈夫曼编码,哈弗曼编码是一种编码方式,能够让原始信息的编码长度,更短一些,从而节省存储空间和传输带宽,是一种无损压缩
基本术语
1、路径和路径长度
在一棵树中,从一个结点往下可以达到的孩子或孙子结点之间的通路,称为路径。
通路中分支的数目称为路径长度。
- 若规定根结点的层数为1,则从根结点到第L层结点的路径长度为L-1。
2、结点的权及带权路径长度
若将树中结点赋给一个有着某种含义的数值,则这个数值称为该结点的权。
结点的带权路径长度为:
- 从根结点到该结点之间的路径长度与该结点的权的乘积。
3、树的带权路径长度
树的带权路径长度规定为所有叶子结点的带权路径长度之和,记为WPL。
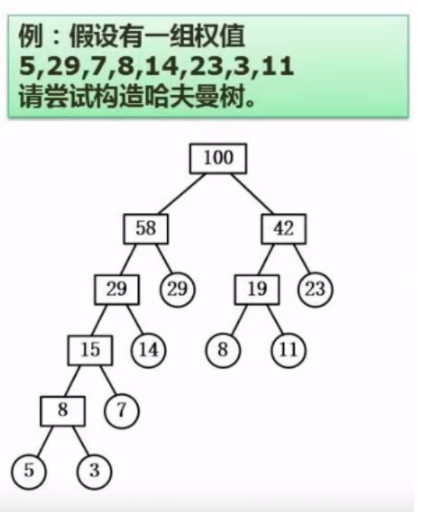
例题
6.4.9、线索二叉树
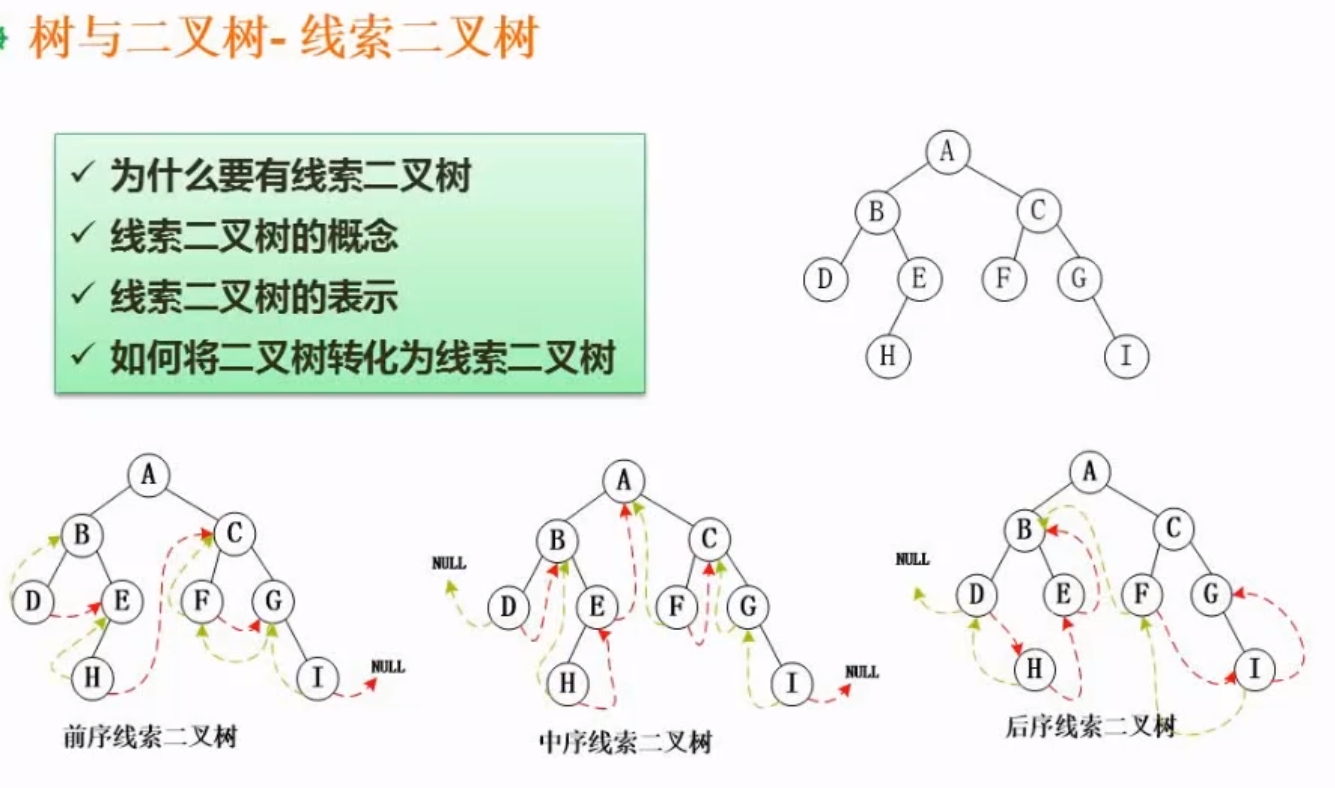
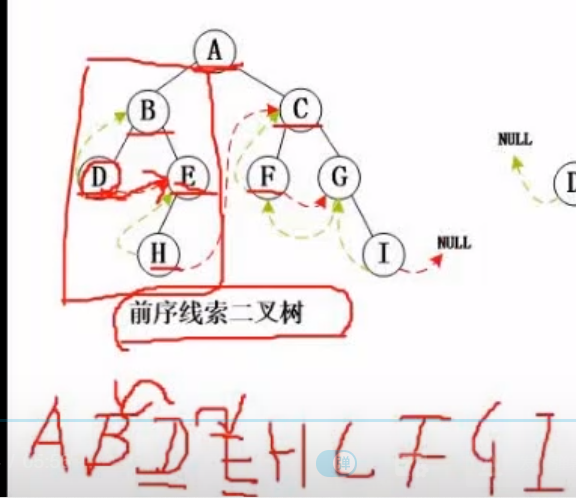
例题
先按照题目的要求将树转化成相应的序列,然后在进行线索的填充
本质
二叉树的遍历本质上是将一个复杂的非线性结构转换为线性结构,使每个结点都有了唯一前驱和后继(第一个结点无前驱,最后一个结点无后继)。对于二叉树的一个结点,查找其左右子女是方便的,其前驱后继只有在遍历中得到。为了容易找到前驱和后继,有两种方法。一是在结点结构中增加向前和向后的指针,这种方法增加了存储开销,不可取;二是利用二叉树的空链指针。
优势与不足
优势
- 利用线索二叉树进行中序遍历时,不必采用堆栈处理,速度较一般二叉树的遍历速度快,且节约存储空间。
- 任意一个结点都能直接找到它的前驱和后继结点。
不足
- 结点的插入和删除麻烦,且速度也较慢。
- 线索子树不能共用。
6.4.10、平衡二叉树
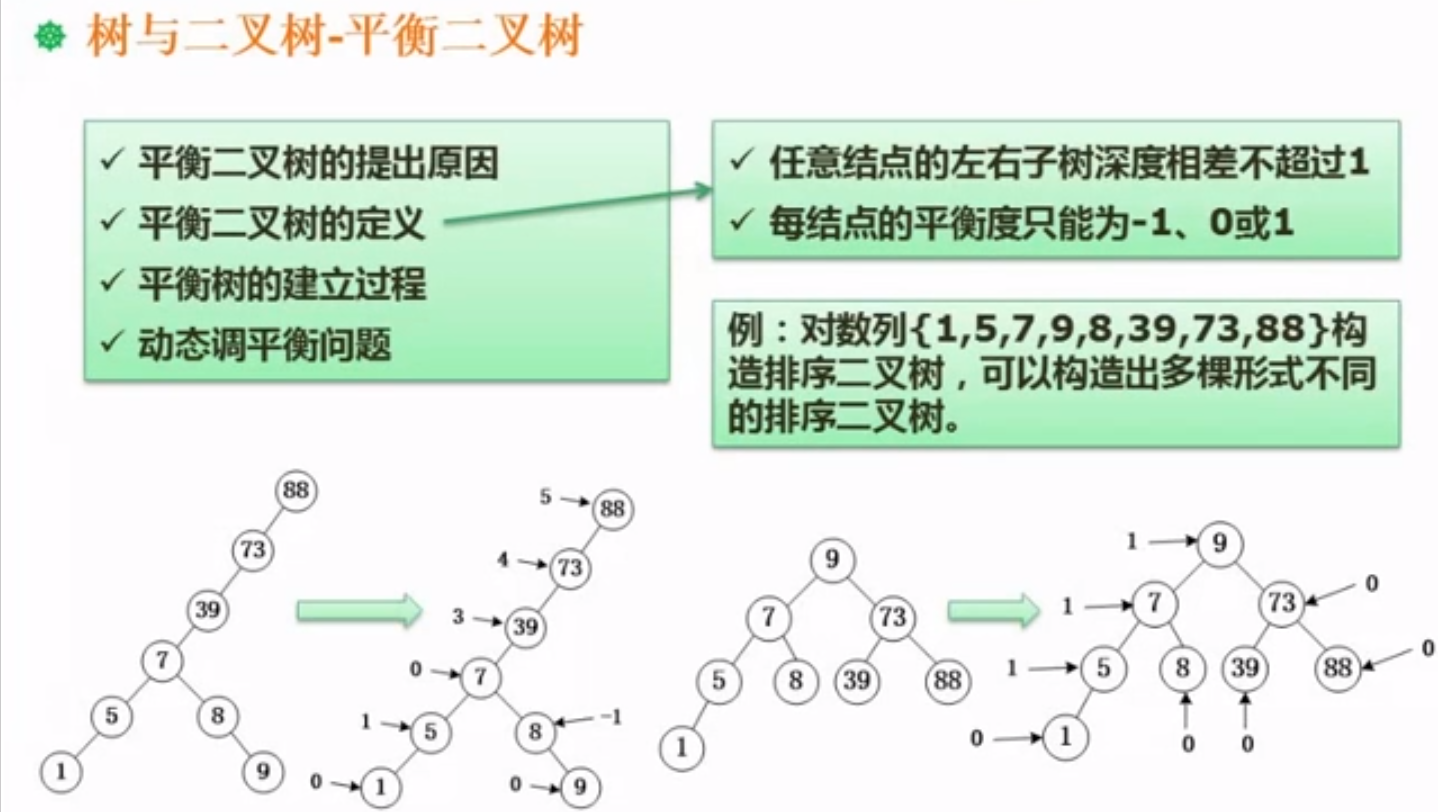
- 平衡二叉树提出的原因
- 同一个序列排序二叉树可能有多个,例如上图当中的最左边的和最右边的二叉树都是查询二叉树 ,平衡二叉树就增加了查询的效率
- 平衡二叉树的定义
- 任意结点的左右子树深度相差不超过1
- 每结点的平衡度只能为-1、0、1
- 平衡度算法 左子树的深度减去右子树的深度得到的就是该平衡树的深度
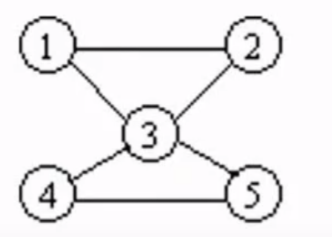
6.5、图
了解基本概念等皮毛的知识
6.5.1、基本概念
无向图:图之间的联系无方向,
有向图:图之间的联系通过有向的箭头相连
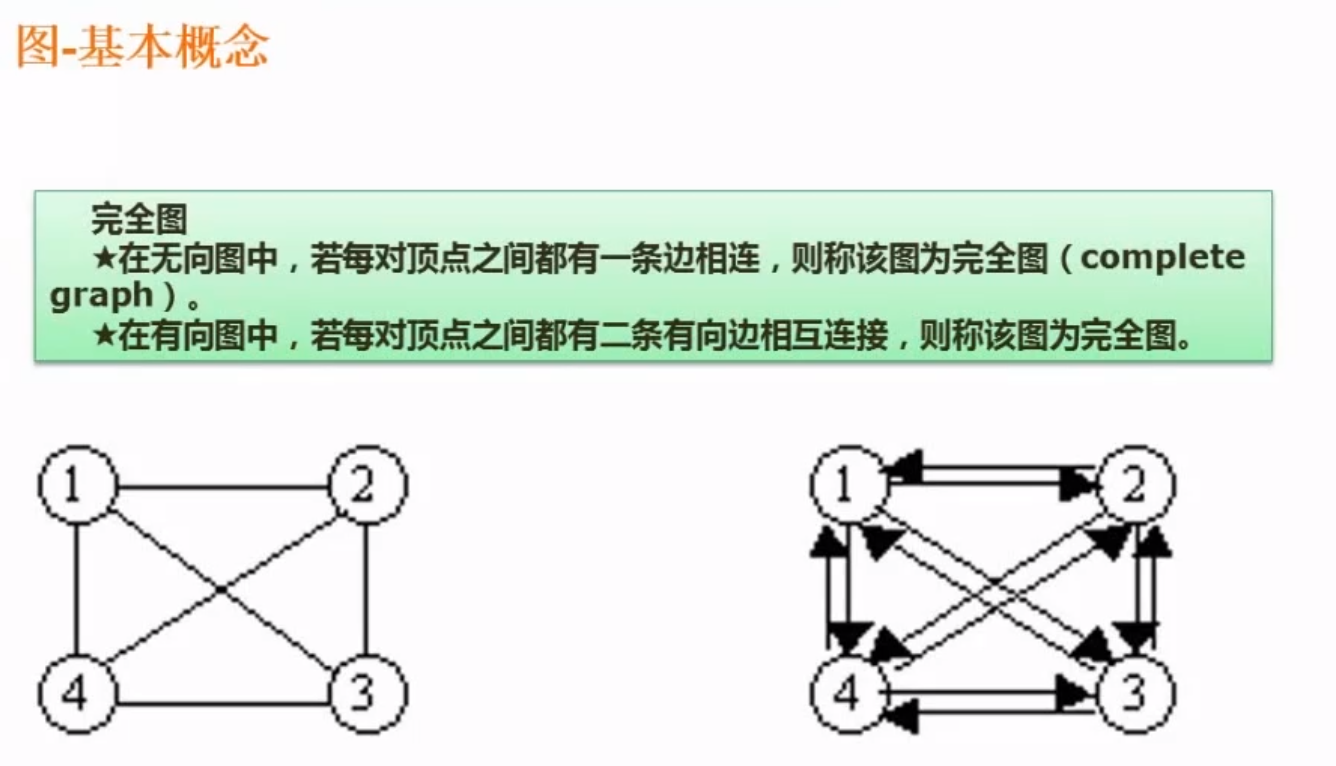
完全图
- 在无向图中,若每对顶点之间都有一条边相连,则称该图为完全图( complete graph).
- 在有向图中,若每对顶点之间都有二条有向边相互连接,则称该图为完全图
6.5.2、图的存储
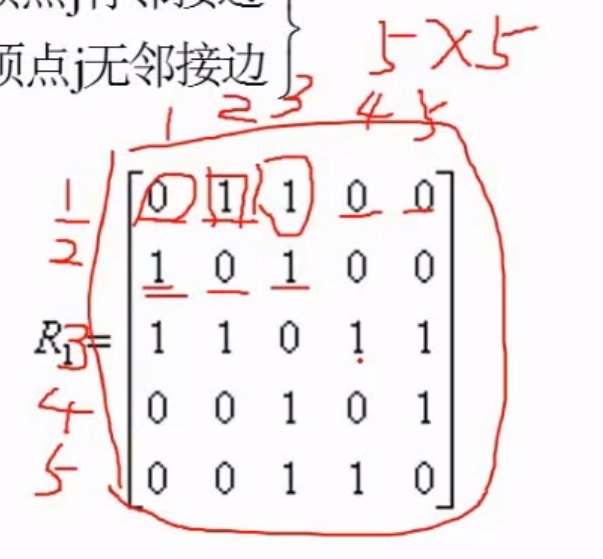
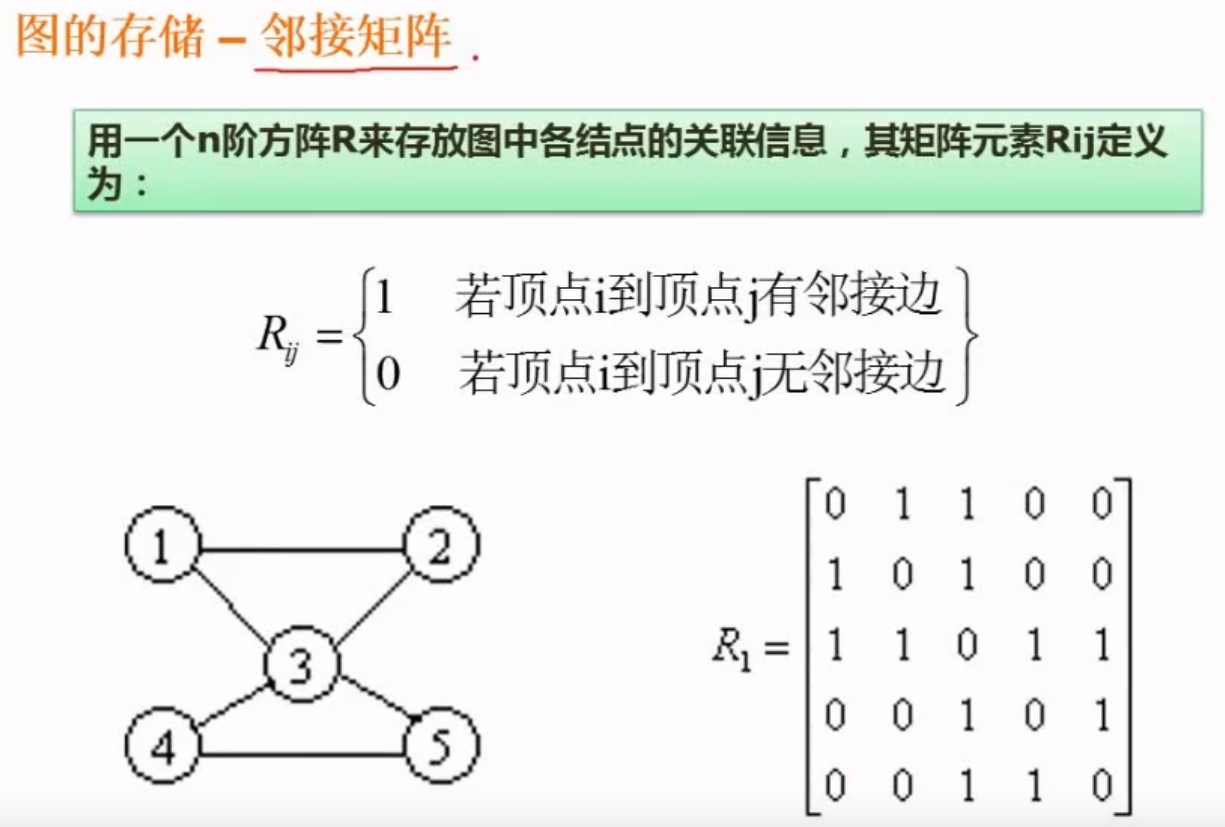
邻接矩阵
例题
因为上图有五个结点所以这个矩阵就是五乘以五的矩阵 ,横竖分别表示对应的编号 ,而其中的值表示这两条边之间是否有联系
对于无向图而言邻接矩阵是对称的所以可以只存上三角也可以只存下三角,这样可以节省存储空间
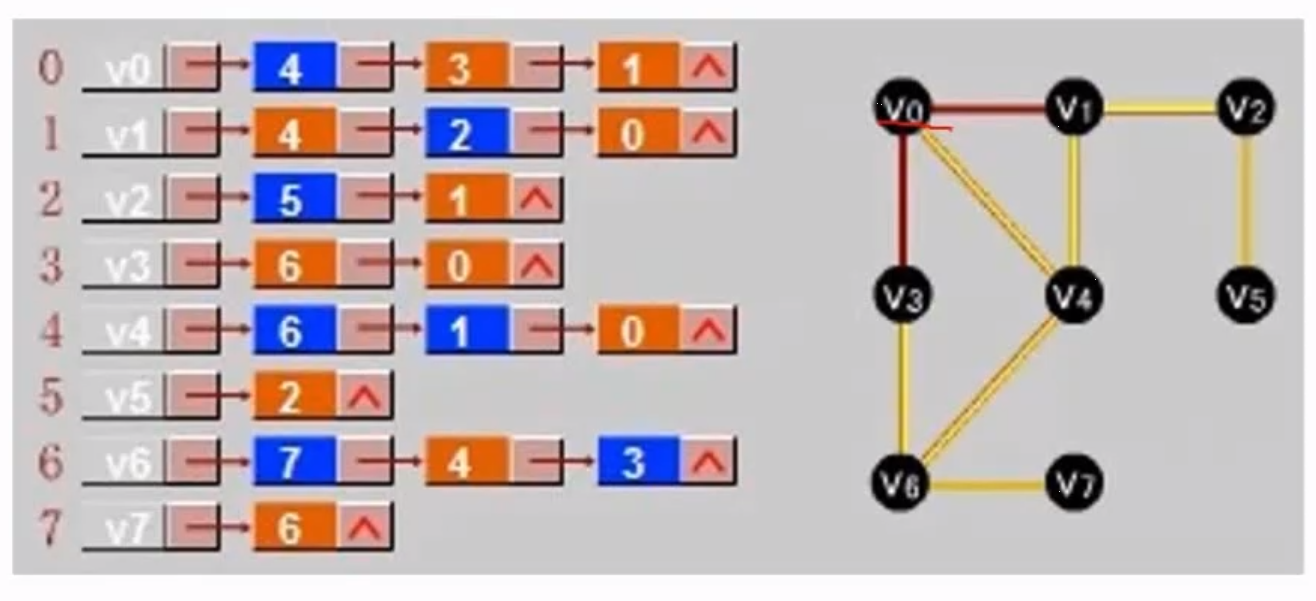
6.5.3、邻接表
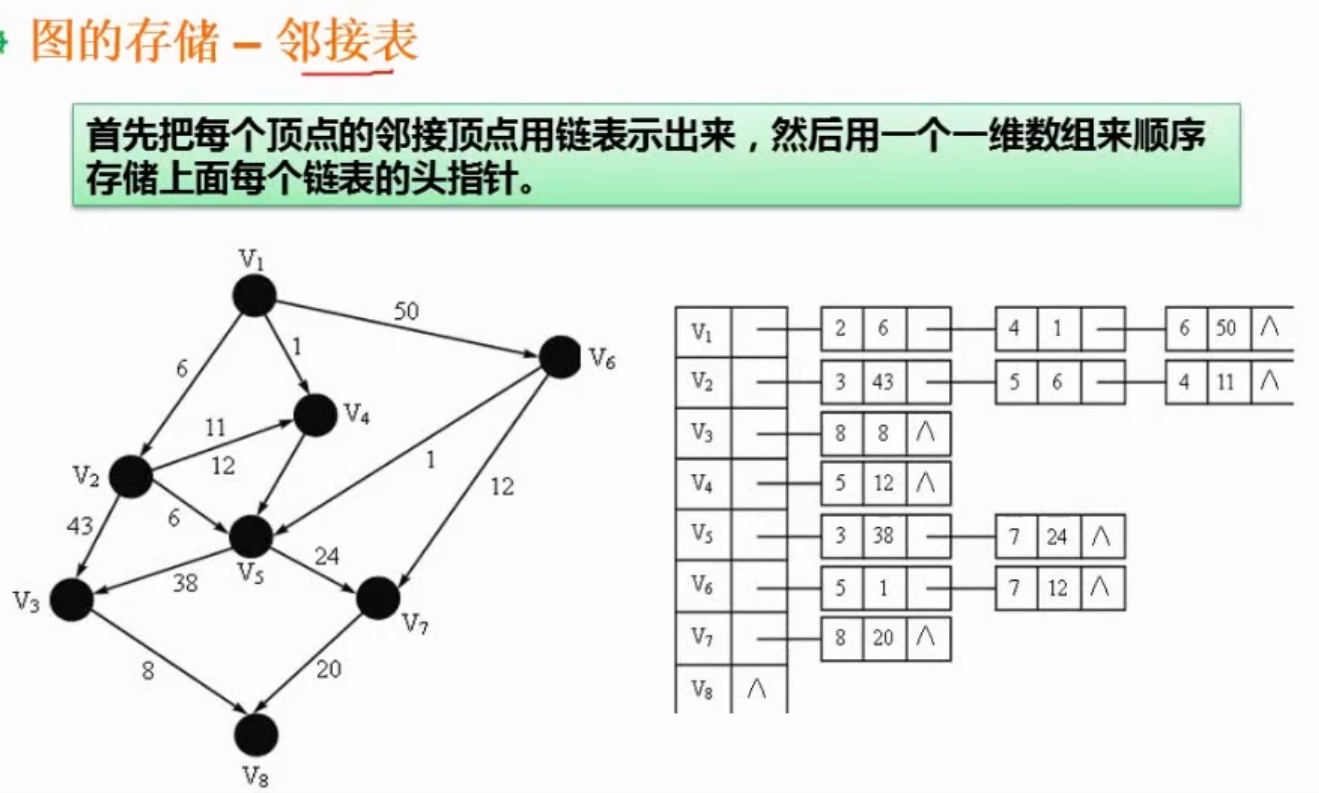
首先用一个表记录所有的结点,用链表的形式将每个结点能够链接的结点写出来
例题
例如从v1 到V2 距离是6 到v4距离是1 到v6 距离是50 就这样写
6.5.4、图的遍历
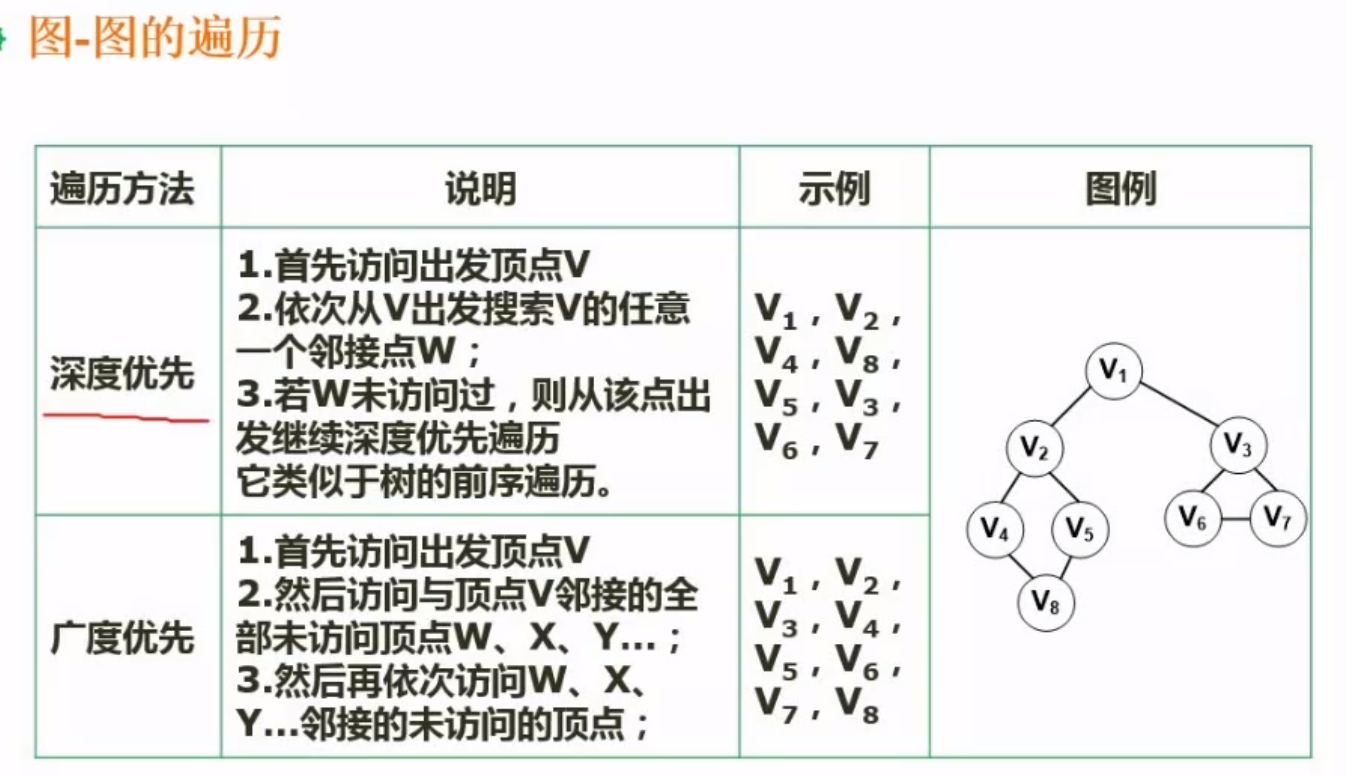
遍历方法
- 深度优先
- 首先访问出发顶点V
- 依次从V出发搜索V的任意一个邻接点W;
- 若W未访向过,则从该点出发继续深度优先遍历它类似于树的前序遍历。
- 广度优先
- 首先访问出发顶点V
- 然后访向与页点V接的全部末访向顶点W、X、Y
- 然后再依次访向W、X、Y.邻接的未访问的顶点;
例题
?????
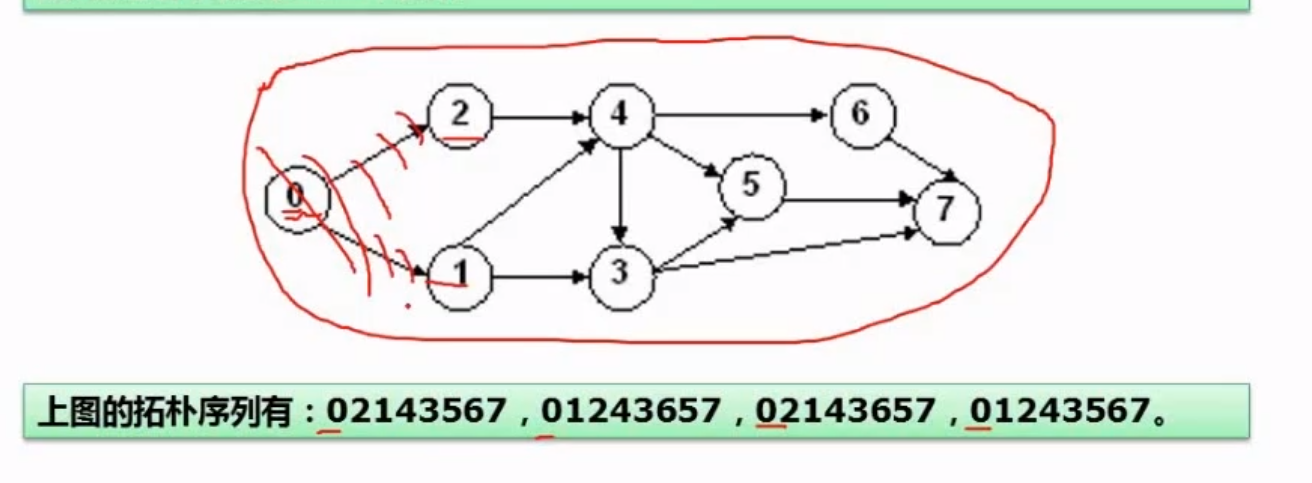
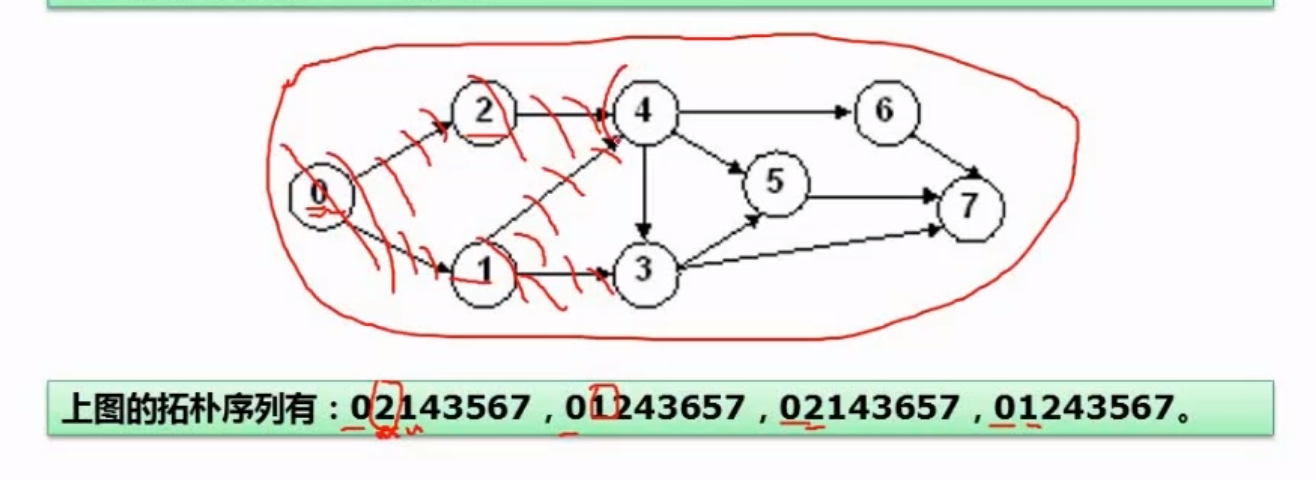
6.5.5、拓扑排序
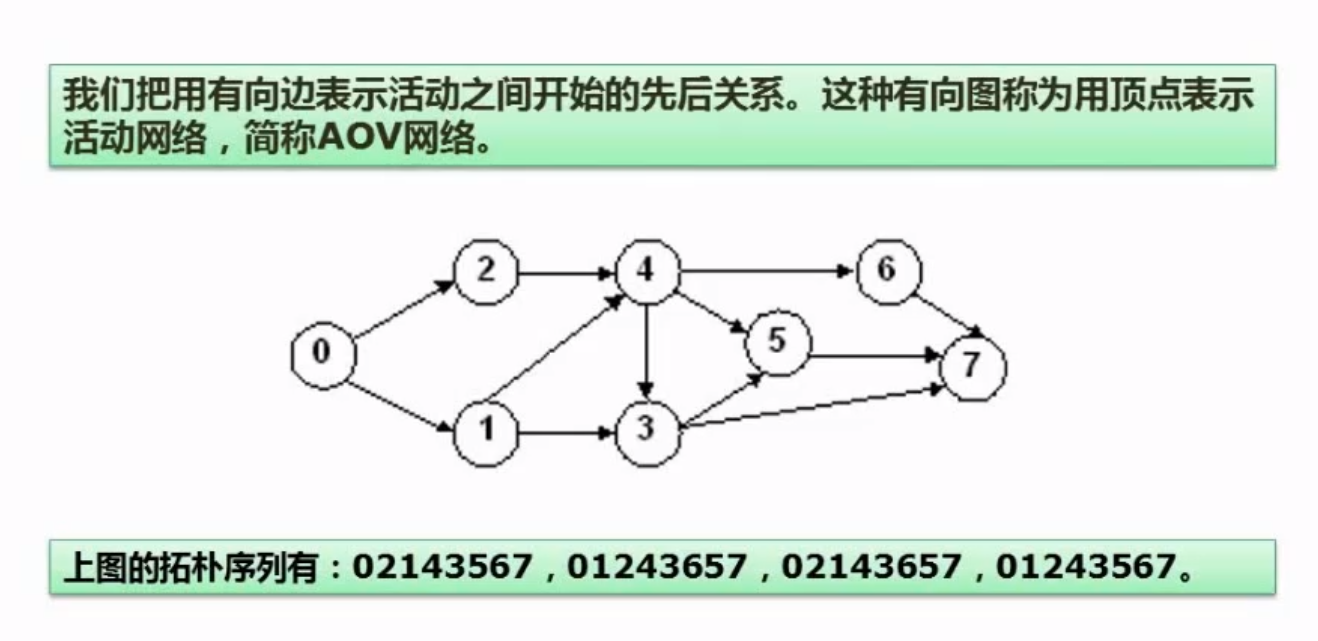
解析:
因为0不受约束 ,所以0先执行,执行之后将0有关的线划掉
这是后1和2 就不收任何的约束了,就可以执行1或者2 执行之后再将相应的线划掉
等1 和2 执行之后4可以执行,执行之后继续划掉,重复这样的操作就可以得出拓扑序列
这一类往往给几个序列,说明哪一个不是这个图的拓扑排序
6.5.6、图的最小生成树-普利姆算法
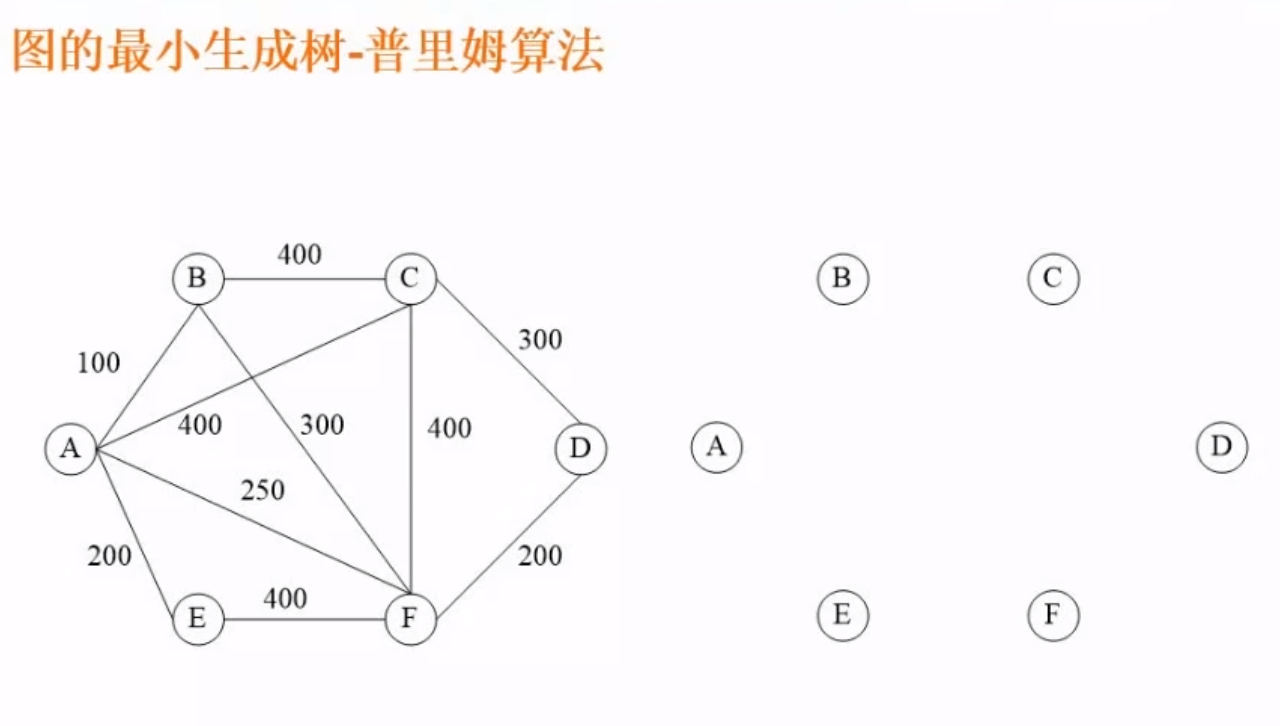
- 树和图的区别
- 树是没有环路的
- 图是有环路的
树如果有n个结点,那么他最多有n-1条边,如果边的条数大于n那么他就是一个图了
- 求最小生成树有两种算法
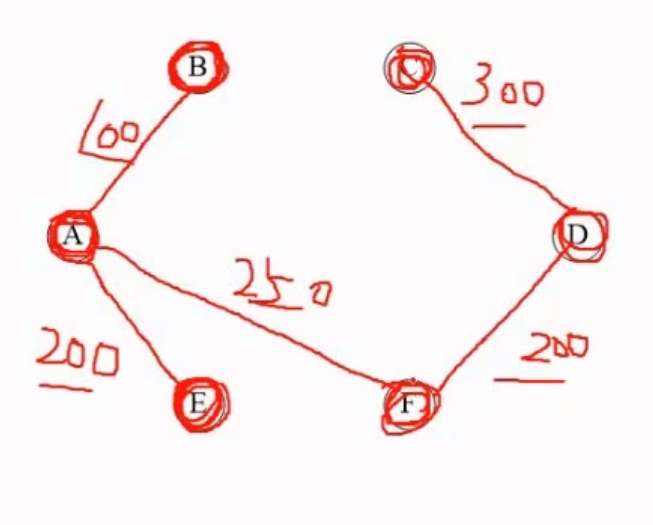
- 普里姆算法
- 从一个结点出发,可以是任意的结点,把第一个点定为红点集,其他的点定为蓝点集
- 找出红点集到蓝点集最短的距离
- 找到最短的距离之后,将这个红点和蓝点进行连线,与红点集相连的这个蓝点就变成了红点
- 继续找红点到蓝点最短的距离,重复上述操作
- 注意
- 这里面的连线不能 形成环
- 克鲁斯卡尔算法
- 我们已知有六个结点,五条边
- 那么就在图中找最小的边,标出来,只要不形成环就标记出来
- 最终也可以生成最小树
- 普里姆算法
普里姆算法的解题方式
克鲁斯卡尔算法解题方式
6.6、查找
6.6.1、算法的特性

- 有穷性:
- 执行有穷步之后结束。
- 确定性:
- 算法中每一条指令都必须有确切的含义,不能含糊不清。
- 输入(>=0)
- 该算法至少有0个输入值
- 输出(>=1)
- 拥有一个及其以上的输出值
- 有效性:算法的每个步骤都能有效执行并能得到确定的结果。
- 例如a=0,b/a就无效
6.6.2、算法的复杂度

- 常见的对算法执行所需时间的度量:
- o(1)<0(log2n)<0(n)<0(nlog2n)<0(n2)<0(n)<0(2n)
- 可以用常数表达的时间复杂度 我们都用 O(1)来表示
- 如果有一个for循环,那么他的执行次数是n次,我们就将这一类的记为O(n)
- 我们取式子的最高次方

6.6.3、顺序查找和二分查找


二分查找要求
- 顺序排列
特点
- 折半查找在査找成功时关键字的比较次数最多为(log2n)+1次。
- 折半查找的时间复杂度为O(log2n)。
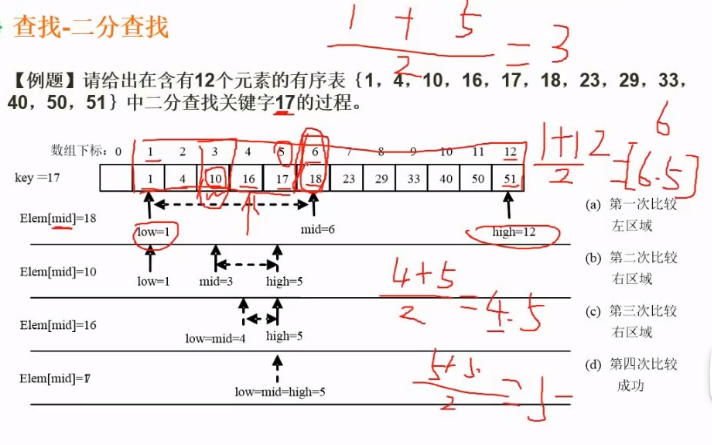
例题
第一次
(1 + 12)/2 = 6.5 = 6 (向下) 取整
第二次
(1+ 5)/ 2 = 3
二分查找注事项
- 首尾相加除以2 如果是小数就向下取整
- 因为中间数是已经比较过得数字了,所以在下一次比较的时候不用比较
6.6.4、散列表
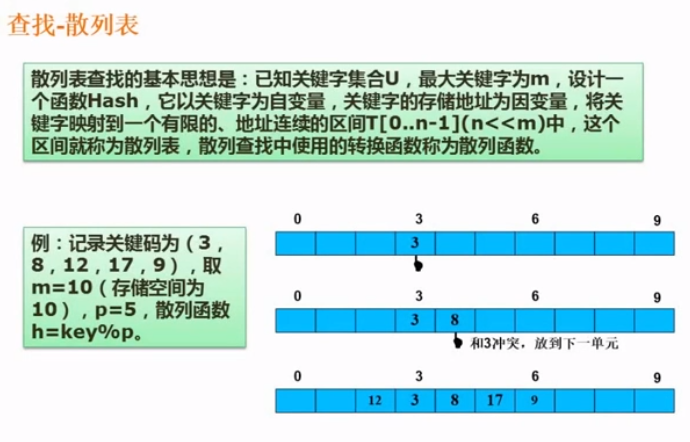
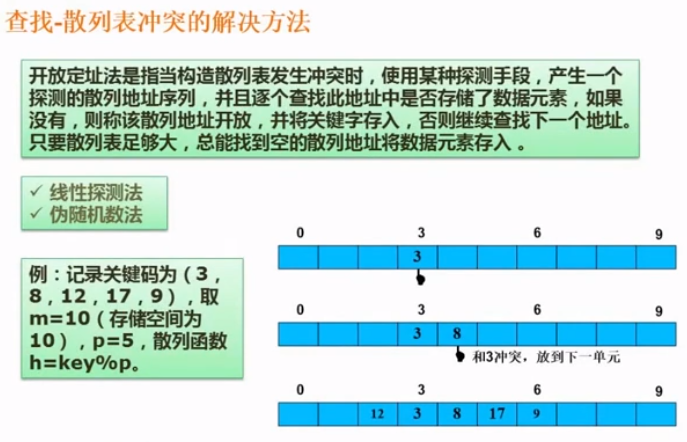
线性探测法:
- 当前空间若是被占了,就移动到下一个空间,如果还是被占了,继续往下移动
6.7、排序

稳定与不稳定排序
- 稳定的排序
- 上图中的一系列数字,有两个21 如果是稳定的排序,排完之后,黑色的21仍然在红色的之前,不稳地的排序,排出来的结果就不一定了
内排序和外排序
- 内排序: 是指在内存中进行排序
- 外排序: 会涉及到外部的存储空间
6.7.1、排序方法的分类
- 插入类排序
- 直接插入排序
- 希尔排序
- 交换类排序
- 冒泡排序
- 快速排序
- 选择类排序
- 简单选择排序
- 堆排序
6.7.2、直接插入排序
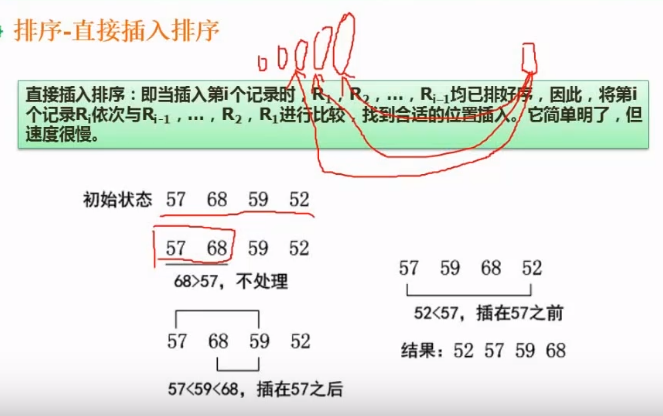

6.7.3、希尔排序
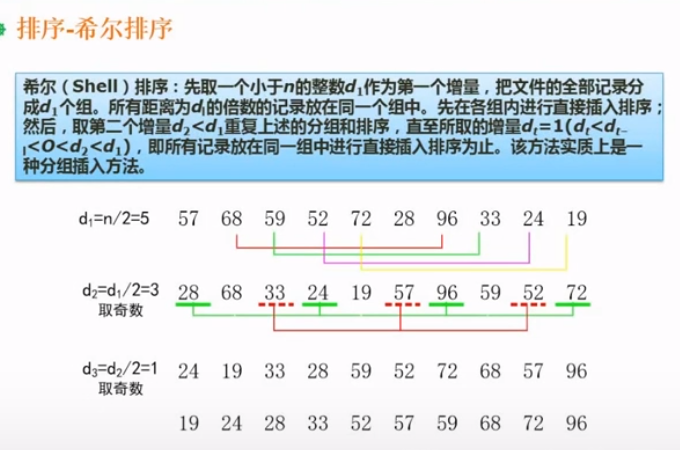
6.7.4、直接选择排序

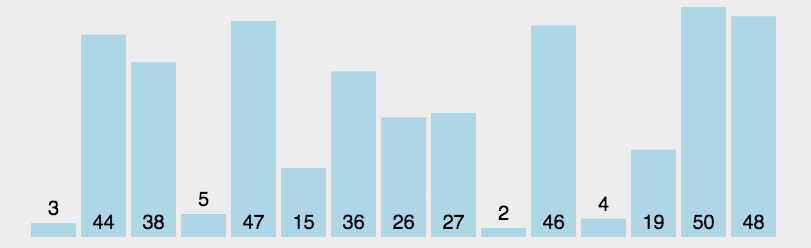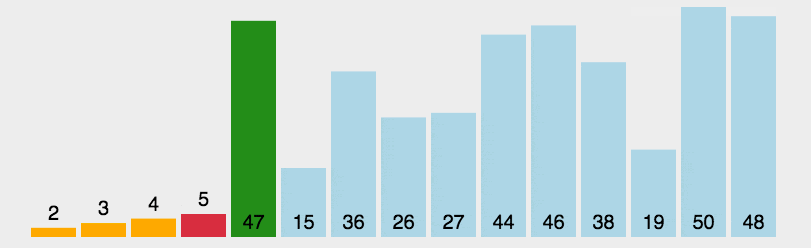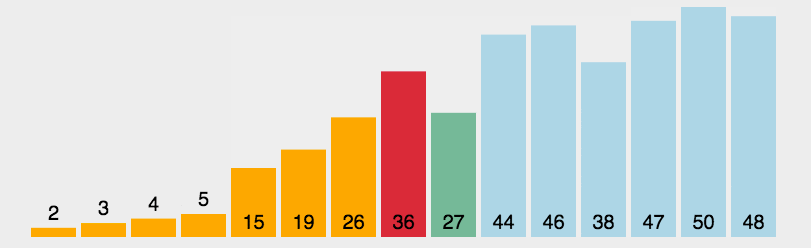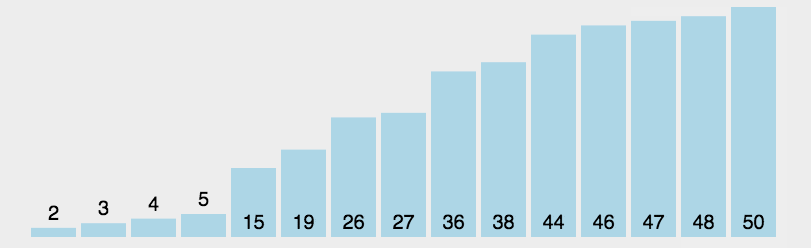
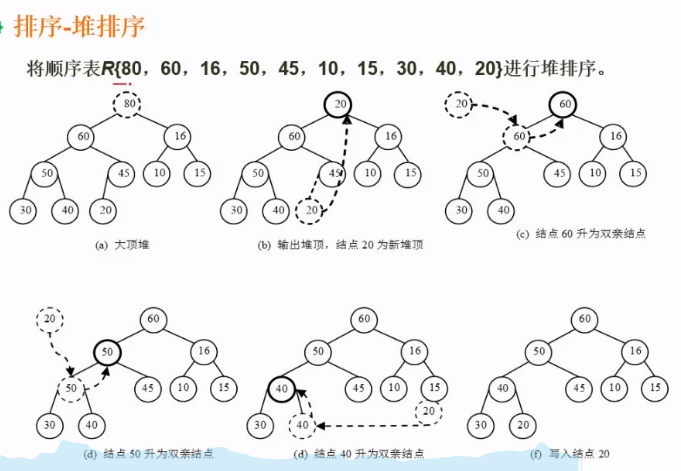
6.7.5、堆排序
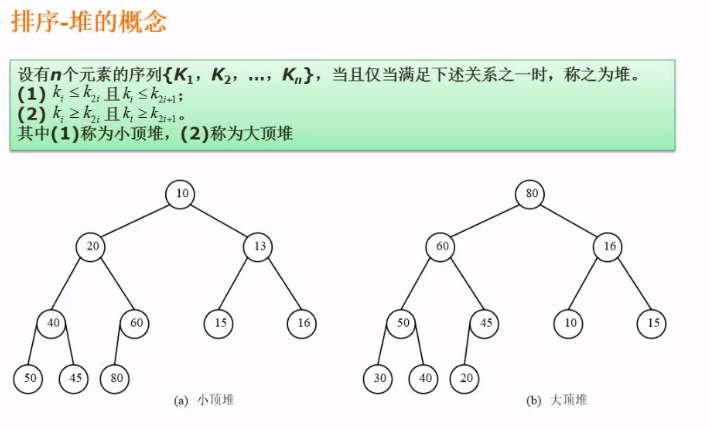
k2i就是ki的左子树
K2i+1是ki的右子树
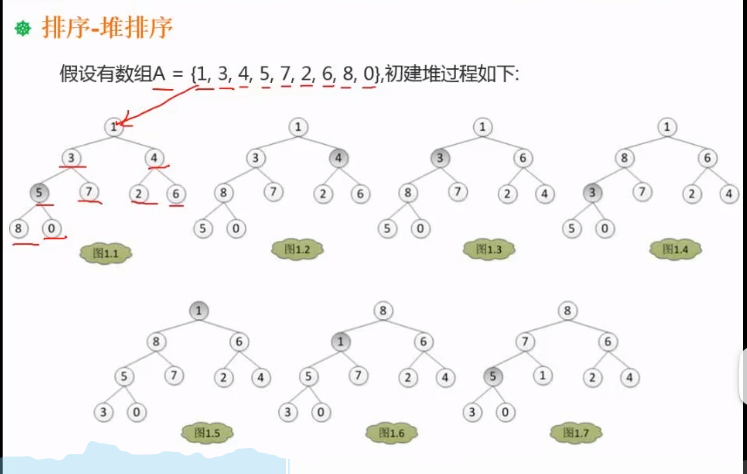
初建堆
- 先顺次按照完全二叉树去建堆(得到图1.1)
- 然后从最后一个非叶子节点开始创建,例图中是5,因为5小于其中一个孩子,所以将5和孩子中的最大值进行交换(得到图1.2)
- 然后调整倒数第二个非叶子节点(结点4),看该节点跟孩子节点想比是不是最大值,不是最大值就和最大值进行交换(图1.3)
- 然后调整3 调整之后得到(图1.4),然后发现下面的结点(3、5、0)还需要调整(得到图1.4)
- 调整3、5、0得到(图1.5)
- 然后开始调整根节点1和8点换位置d得到(图1.6)
- 调整1和7 得到(图1.7)
删除结点之后的堆重排

6.7.6、冒泡排序

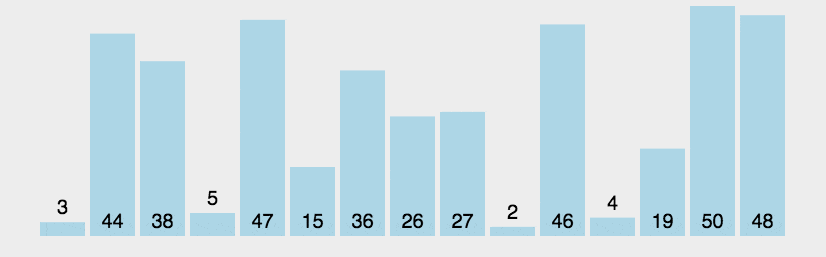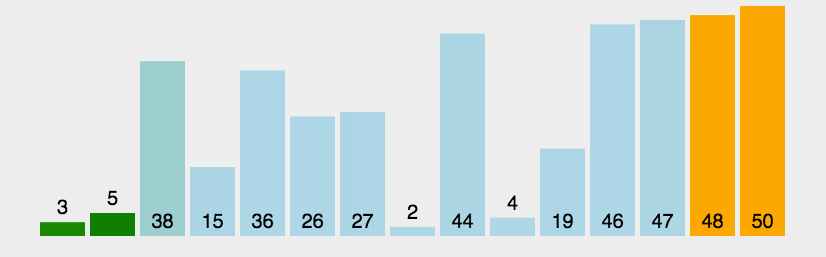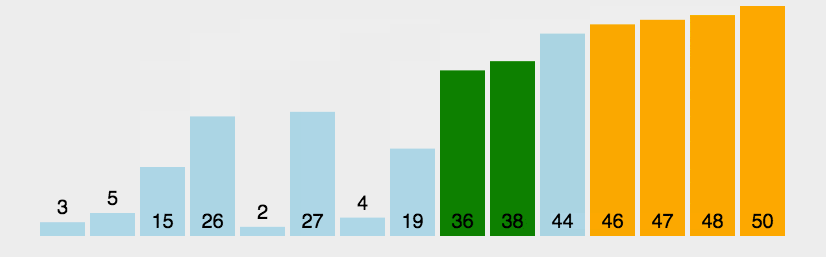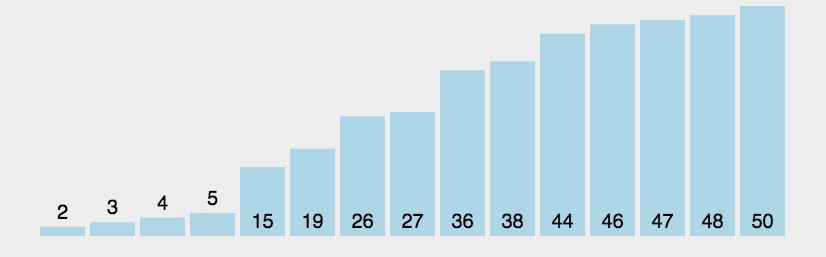
6.7.7、快速排序

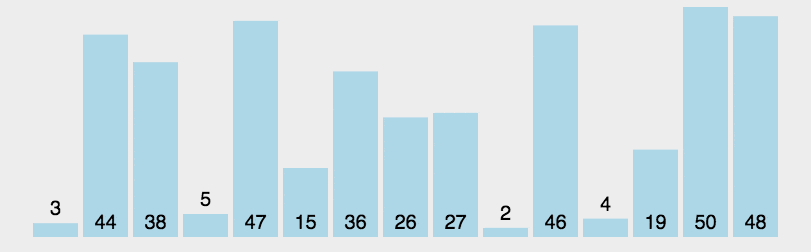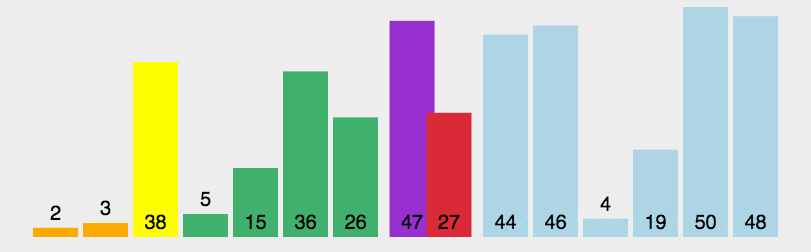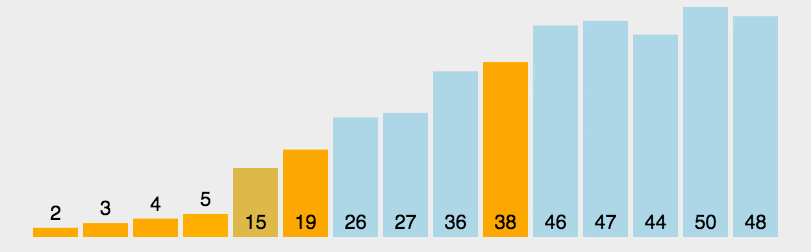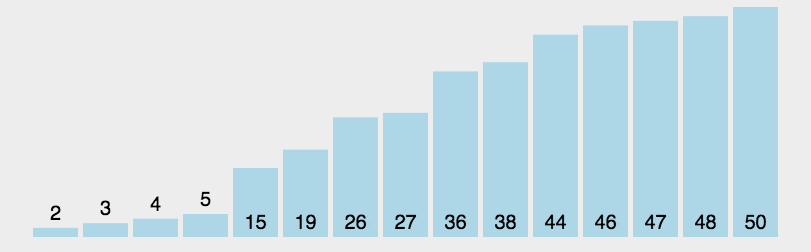
先选定一个(第一个)数为基准,然后根最后一个比较,如果最后一个比基准小,就将基准和这个数进行交换,交换之后基准和正数第二个进行比较,如果基准大于第二个数则和第三个数进行交换,直到有个数字大于基准,则将基准换到前面,基准则和倒数第二个数进行排序,同理进行比大小,直至基准无法移动为止,然后左右两边的值递归进行快排
6.7.8、归并排序

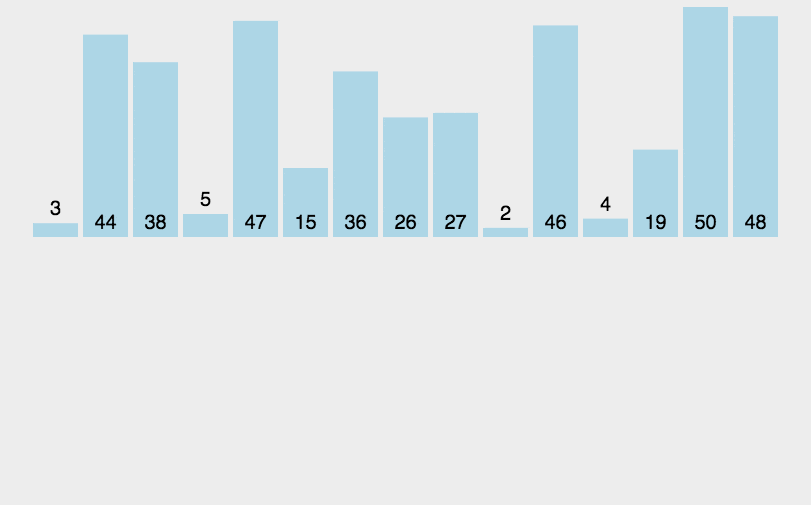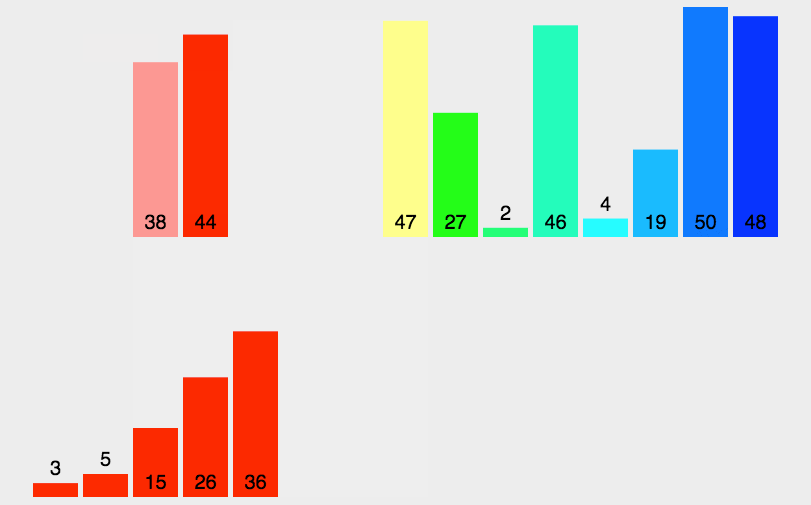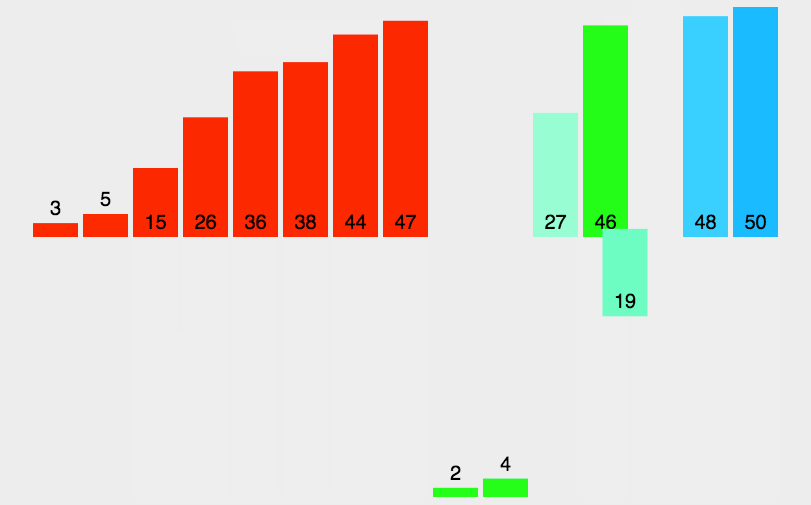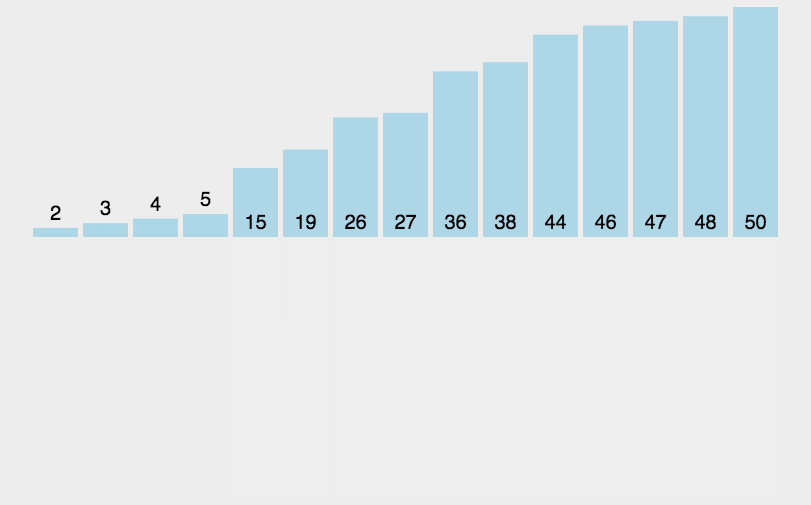
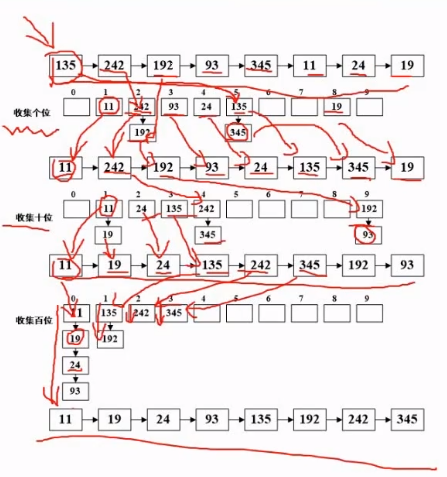
6.7.9、基数排序
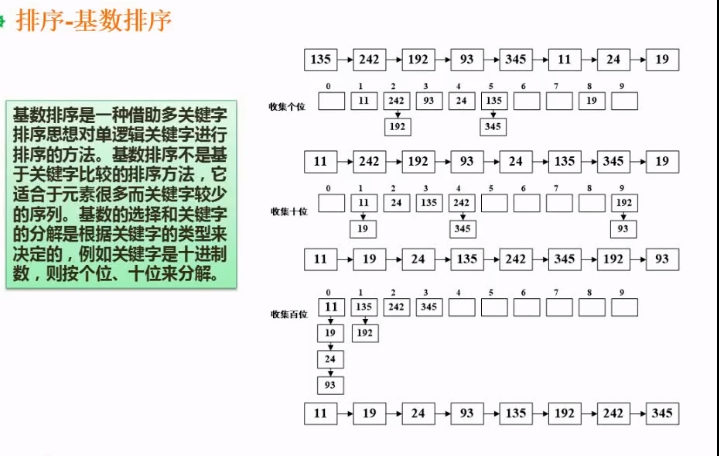
先排个位数,在排十位数,再排百位数以此类推.

6.8、算法基础及常见的算法