参考资料：

二叉树遍历口诀

二叉树遍历：

在了解了递归书写原理和执行原理后，进行实践的规律总结，以下面二叉树遍历为例，相关代码会在文章后面贴出。

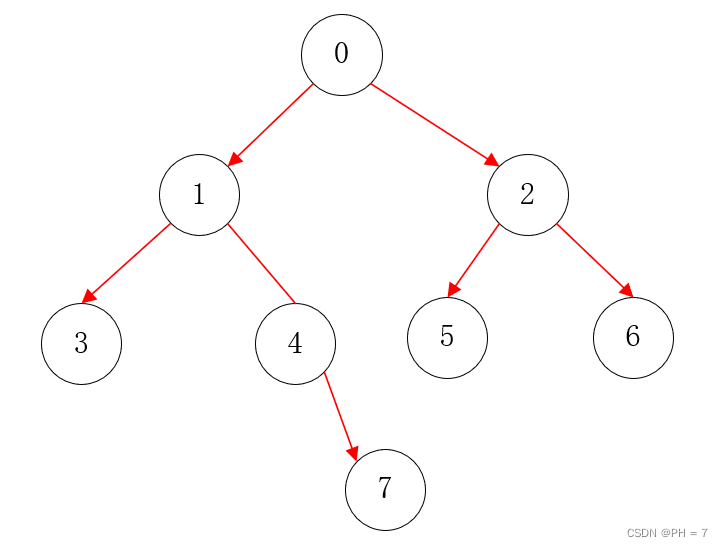
 二叉树遍历分为：深度遍历和层级遍历

二叉树深度遍历

• 二叉树深度遍历分为前序遍历，中序遍历和后序遍历
• 前序遍历的口诀为：根左右
• 中序遍历的口诀为：左根右
• 后序遍历的口诀为：左右根
• 下面是他们的具体实现代码

1.  前序遍历口诀：根左右

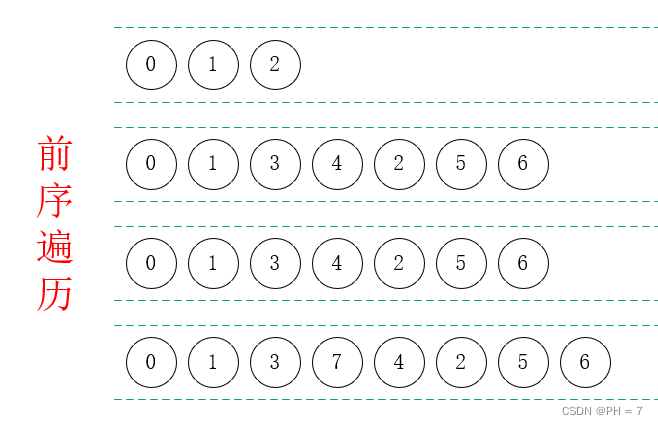
•  首先从根节点开始，根左右：0，1，2
• 然后以1为根，根左右：1，3，4，结果变为：0，1，3，4，2
• 然后以2为根，根左右：2，5，6，结果变为：0，1，3，4，2，5，6
• 然后以3为根，根左右：3，null,7，结果变为：0，1，3，7，4，2，5，6
• 然后以4为根，根左右：4，null，null，null值不计，结果不变
• 然后以5为根，根左右：5，null，null，null值不计，结果不变
• 然后以6为根，根左右：6，null，null，null值不计，结果不变
• 然后以7为根，根左右：7，null，null，null值不计，结果不变

所以，上述二叉树的前序遍历结果为

0，1，3，7，4，2，5，6

即，前序遍历代码输出结果同上

    //前序遍历public void deepSortOutFont(TreeNode node){if(node == null){return;}System.out.println("前序遍历为："+node.val);deepSortOutFont(node.left);deepSortOutFont(node.right);}

1.  中序遍历口诀：左根右

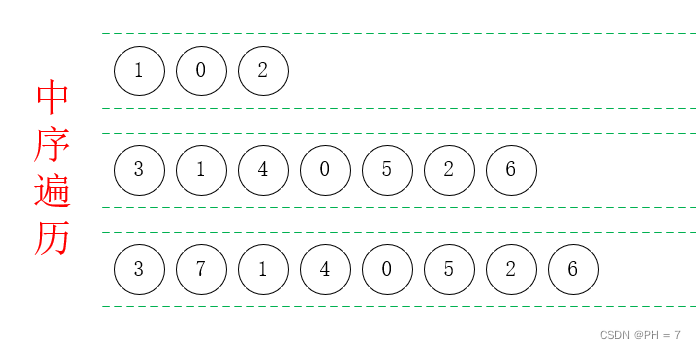
•  首先从根节点开始，左右根：1，0，2
• 以未遍历的节点1为根节点，左右根：3，1，4，结果为：3，1，4，0，2
• 以未遍历的节点2为根节点，左右根：5，2，6，结果为：3，1，4，0，5，2，6，
• 以未遍历的节点3为根节点，左右根：null，3，7，结果为：3，7，1，4，0，5，2，6
• 以未遍历的节点4为根节点，左右根：null，4，null，null值不计，结果不变
• ... ...
• 以未遍历的节点7为根节点，左右根：null，7，null，null值不计，结果不变

所以，上述二叉树的中序遍历的结果为：

3，7，1，4，0，5，2，6

即，中序遍历代码结果同上

    //中序遍历public void deepSortOutMiddle(TreeNode node){if(node == null){return;}deepSortOutMiddle(node.left);System.out.println("中序遍历为："+node.val);deepSortOutMiddle(node.right);}

1. 后序遍历口诀：左右根

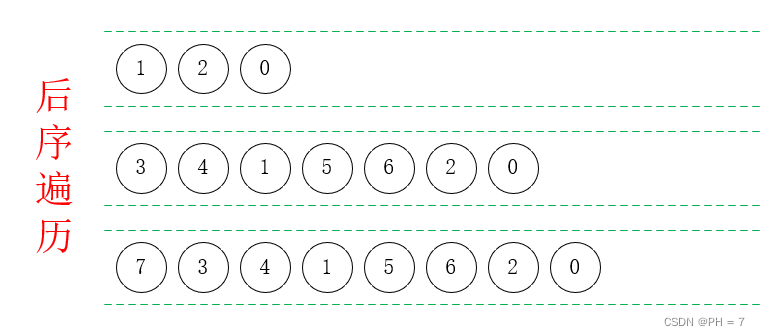
•  首先从根节点开始，左右根：1，2，0
• 以未遍历节点1为根，左右根：3，4，1，结果为：3，4，1，2，0
• 以未遍历节点2为根，左右根：5，6，2，结果为：3，4，1，5，6，2，0
• 以未遍历节点3为根，左右根：null，7，3，结果为：7，3，4，1，5，6，2，0
• 以未遍历节点4为根，左右根：null,null,4，null值不计，结果不变
• 以未遍历节点5为根，左右根：null,null,5，null值不计，结果不变
• 以未遍历节点6为根，左右根：null,null,6，null值不计，结果不变
• 以未遍历节点7为根，左右根：null,null,7，null值不计，结果不变

所以，上述二叉树的后序遍历的结果为：

7，3，4，1，5，6，2，0

即，后序遍历代码结果同上

    // 后序遍历public void deepSortOutAfter(TreeNode node){if(node == null){return;}deepSortOutAfter(node.left);deepSortOutAfter(node.right);System.out.println("后序遍历为："+node.val);}

1. 总结

• 二叉树前、中、后序遍历，都是从根节点开始，按照口诀：根左右、左根右、左右根进行遍历

二叉树层序遍历

层序遍历是利用栈的特点，优先遍历节点旁边的节点，依次类推，蔓延下去，具体代码如下：

层序遍历的 过程如下：

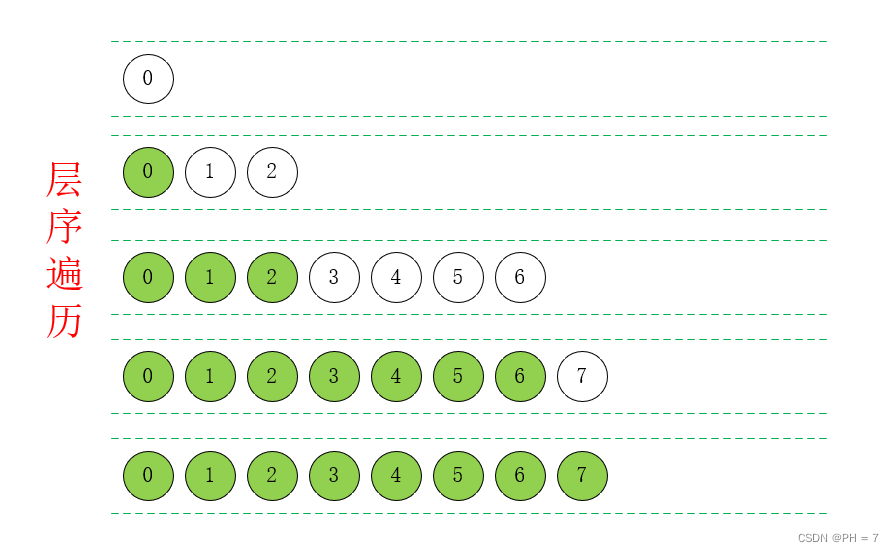
• 首先从根节点开始，0，结果为：0
• 然后0附近的两个点 ，1，2，结果为：0，1，2
• 然后1附近的两个点，3，4，结果为：0，1，2，3，4
• 然后2附近的两个点，5，6，结果为：0，1，2，3，4，5，6
• 然后3附近的两个点，null,7,结果为：0，1，2，3，4，5，6，7
• 然后4，5，6，7附近的两个点，null，null，null值不计，结果不变

所以层序遍历的结果为：

0，1，2，3，4，5，6，7

即上述层序遍历的代码的执行结果同上

    //层序遍历public void layerTranverse(TreeNode root){if(root == null){return;}Queue q = new LinkedList();q.add(root);while(!q.isEmpty()){TreeNode n = q.poll();System.out.println(n.val);if(n.left!=null){q.add(n.left);}if(n.right != null){q.add(n.right);}}}

 二叉树遍历到递归的应用：

上述我们已经掌握了二叉树深度遍历的口诀及应用，拓展至递归函数中，相对于用递归原理理解有着简单易用，具有很强的实践性。

那么我们应该怎样用这个规律，去理解，解析，并将递归函数转化为普通函数呢？

下面将以归并排序为例，进行讲解：

归并排序的基本代码为：

    public static void mergeSort(int array[], int left, int right) {if (left < right) {int middle = (left + right) / 2;// System.out.println("前序遍历："+Arrays.toString(array));mergeSort(array, left, middle);//System.out.println("中序遍历："+Arrays.toString(array));mergeSort(array, middle + 1, right);//System.out.println("后序遍历："+Arrays.toString(array));merge(array, left, middle, right);}}

 mearge函数的意思是，将数组的left下标到right下标进行倒序排序，这里为了方便说明就不写出，文章后面会贴出完整代码，下面将一步步进行分析：

1. 首先我们拿到一个双并列递归，除终止条件和递归函数，其他的全部暂时抹去，得到：

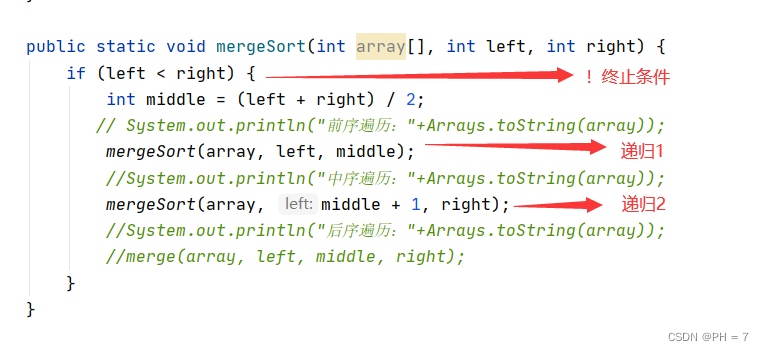
1.  然后我们，输入一个样本数组，并画出二叉树，如：

array：{ 5, 4, 9, 8, 7, 6, 0, 1, 3, 2 }

left：0

right: 9

注意：array的下标是从0开始的

根据函数表述：两个递归函数是将数组的左半部分和右半部分不断分解，直到left>=right（注意终止条件不画出），得到如下二叉树

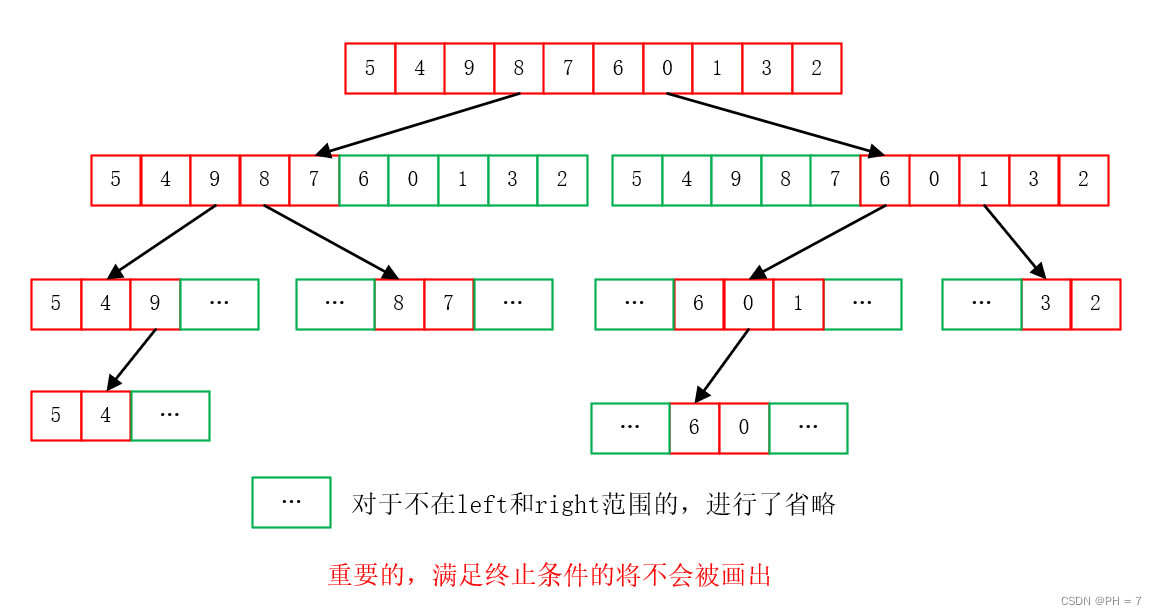
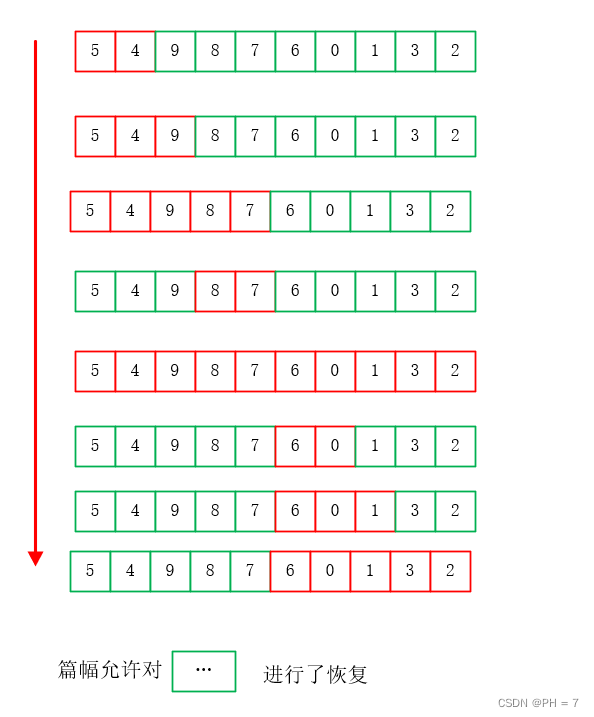
1. 然后我们把要进行的要进行的数据操作放开：如merge函数得到后序遍历

1.  根据后序遍历口诀：左右根，将递归函数转化为非递归函数，得到merge函数的入参顺序，根据merge定义：将下标范围内的数字进行倒序排列，得到每一次入参后的结果

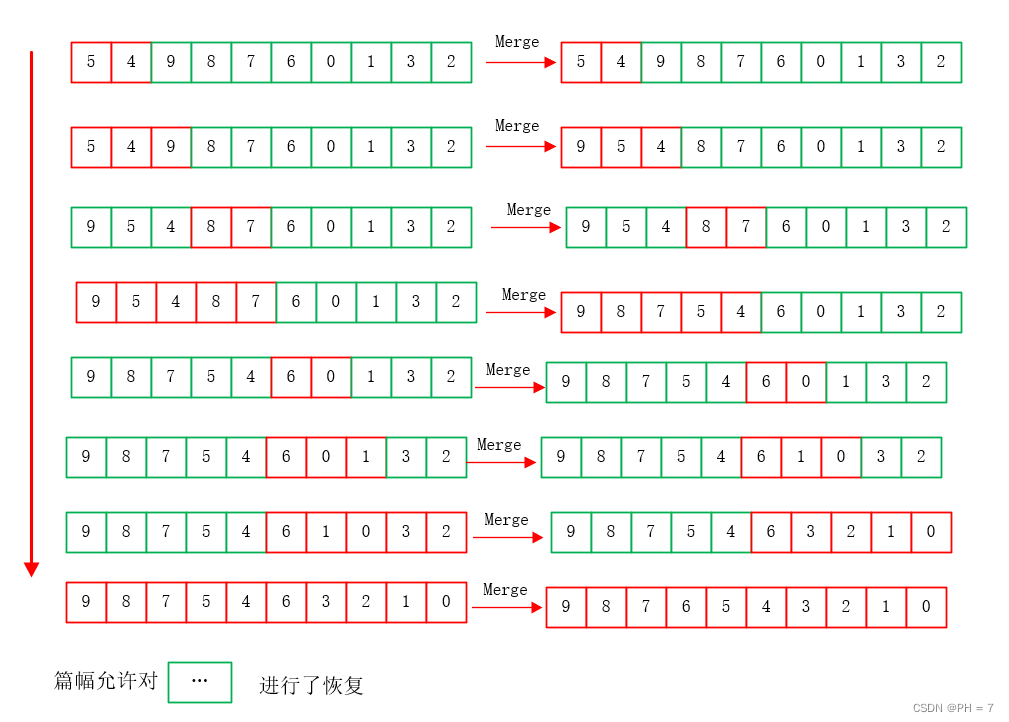
这样，我们就把递归、递推函数改变成了有着不断入参的非递推函数💴

1. 同样，根据二叉树的分解以及执行流程，理解了此归并排序的含义：将数组不断地利用二分法进行分解，直至两个元素，然后再对每一部分进行排序

这样，我们就轻松的对递归函数进行了理解，并且转化为了非递归函数，🦾，相当好用

 再用一遍

在上述例子中，我们把merge函数盖住，将

System.out.println("前序遍历："+Arrays.toString(array));

打开，得到

很明显，这是个前序遍历，根据前面画出的二叉树，根据前序遍历口诀：根左右 ，得到该执行语句的入参