单点时限: 2.0 sec

内存限制: 256 MB

没有人在热河路谈恋爱，
总有人在天亮时伤感
如果年轻时你没来过热河路，
那你现在的生活是不是很幸福
——李志《热河》

奔跑。跌倒。奔跑。

热河路有一家开了好多年的理发店，不管剪什么样的发型，你只要付五块钱。现在我们来到了热河路。

我们可以将其抽象成一个如下的序列：

110100100010000100000……

请你找出这个无穷序列中指定位置上的数字。

输入格式

第一行一个正整数 n (1≤n≤1500000)，表示询问次数。

接下来的 n 行，每行一个正整数 ai (1≤ai≤10^9)，ai 表示在序列中的位置。

输出格式

输出 n 行，每行为一个 0 或 1，表示该序列第 ai 位上的数字。

样例

input

4
3
14
7
6

output

0
0
1
0

解法一：（直接模拟，一般会超时）：

#include 
#include 
#include 
using namespace std;
class SingleJob {public:int seq;};
int main() {int jobs, temp;SingleJob J[1500000];// 输入cin >> jobs;for(int i = 0; i < jobs; i++) {cin >> J[i].seq;}// 输出for(int i = 0; i < jobs; i++) {int level=0;	// 当前段位0的个数int loops=1;	// 当前小节正在读第loops个数字for(int pos=1; pos<=J[i].seq; pos++)	// {if(level == loops || level==0 ){temp = 1;level++;loops = 1;}else{temp = 0;loops++;}}cout << temp <<  endl;}return 0;
}

解法二：Hash方式模拟（缺点是定义数组导致栈空间消耗巨大，在不同的环境下可能会爆栈）

#include 
#include 
#include 
using namespace std;
class SingleJob {public:int seq;
};const int Max = 1e9;
bool HashTable[Max]={false};
int main() {int jobs, temp;SingleJob J[1500000];//输入cin >> jobs;for(int i = 0; i < jobs; i++) {cin >> J[i].seq;}int level = 0;   for(int i = 1;i <= Max;i+=level++) {HashTable[i] = 1;}//输出for(int i = 0; i < jobs; i++) {printf("%d\n", HashTable[J[i].seq]);}return 0;
}

解法三：折中方案（优化了一下，使用set集合，每获得一个"1"的位置就记入该集合）：

这么做能极大地缓解栈空间的压力，省去了一个 10^9 大小的bool型数组。

#include 
#include 
#include 
using namespace std;
class SingleJob {public:int seq;};int main() {int jobs, temp;SingleJob J[1500000];set HashTable;  // 输入scanf("%d", &jobs);for (int i = 0; i < jobs; i++) {scanf("%d", &J[i].seq);}int level = 0;for (int i = 1; i <= 1e9+1; i += level++) {HashTable.insert(i);}// 输出for (int i = 0; i < jobs; i++) {temp = (HashTable.find(J[i].seq) !=  HashTable.end()) ? 1:0;printf("%d\n", temp);}return 0;
}

这里有个坑：如果把 scanf 和 printf 用 cin和cout 代替，会导致

Time limit exceeded on test 10 错误

这个问题的导致原因与 cin和cout方法的一些额外开销有关，不是本题的重点。知道一下cin和cout相对而言确实会慢一点就可以了。

附：三种不同解法的时空开销

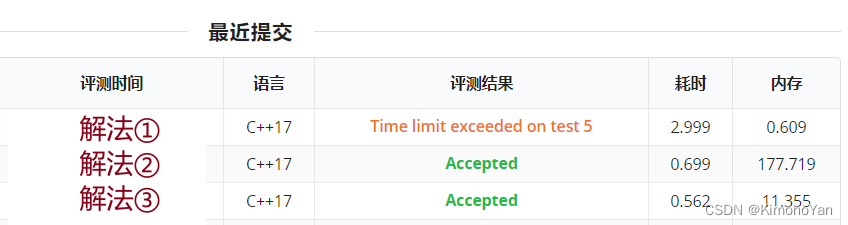
至于你问我 “为什么不用找规律的解法” 。

我的回答是：

.

就不！ovo