跳跃-动态规划问题

• 1、题目描述
• 2、解题思路
• • 2.1 解法一：动态规划
  • 2.2 解法二：DFS深度优先搜索最大权值

1、题目描述

  小蓝在一个 n 行 m 列的方格图中玩一个游戏。

  开始时，小蓝站在方格图的左上角，即第 11 行第 11 列。

  小蓝可以在方格图上走动，走动时，如果当前在第 r 行第 c* 列，他不能走到行号比 r 小的行，也不能走到列号比 c 小的列。同时，他一步走的直线距离不超过 3。

  例如，如果当前小蓝在第 3 行第 5 列，他下一步可以走到第 3 行第 6 列、第 3 行第 7 列、第 3 行第 8 列、第 4 行第 5 列、第 4 行第 6 列、第 4 行第 7 列、第 5 行第 5 列、第 55 行第 6 列、第 6 行第 5 列之一。

  小蓝最终要走到第 n 行第 m 列。

  在图中，有的位置有奖励，走上去即可获得，有的位置有惩罚，走上去就要接受惩罚。奖励和惩罚最终抽象成一个权值，奖励为正，惩罚为负。

  小蓝希望，从第 1 行第 1 列走到第 n 行第 m* 列后，总的权值和最大。请问最大是多少？

  输入描述

  输入的第一行包含两个整数 n,m，表示图的大小。

  接下来 n 行，每行 m* 个整数，表示方格图中每个点的权值。

  其中，1≤n≤100,−104≤权值≤1041\le n\le 100,-10^4\le 权值\le10^41≤n≤100,−104≤权值≤104

  输出描述

  输出一个整数，表示最大权值和。

  输入输出样例

  示例 1

输入

3 5
-4 -5 -10 -3 1
7 5 -9 3 -10
10 -2 6 -10 -4

输出

15

  运行限制

• 最大运行时间：1s
• 最大运行内存: 128M

2、解题思路

2.1 解法一：动态规划

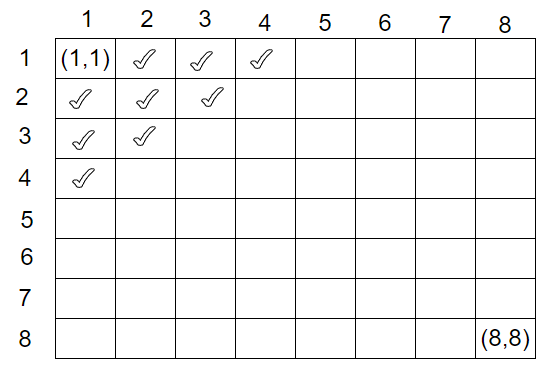
  开始的时候我们站在(1,1)(1,1)(1,1)位置，且一步走的直线距离不超过3，如上图所示，假设我们现在开始在(1,1)(1,1)(1,1)位置，那么我们下一步的位置只能是(1,2),(1,3),(1,4),(2,1),(2,2),(2,3),(3,1),(3,2),(4,1)(1,2),(1,3),(1,4),(2,1),(2,2),(2,3),(3,1),(3,2),(4,1)(1,2),(1,3),(1,4),(2,1),(2,2),(2,3),(3,1),(3,2),(4,1)其中的一个。

  那我们可以由此建立一个搜索的坐标数组，每次从当前位置搜的时候我们就扩展坐标即可。

  令dp[i][j]dp[i][j]dp[i][j]表示从(1,1)(1,1)(1,1)到达(i,j)(i,j)(i,j)位置获得的最大权值。

  但是我们当前位置是由前面九个位置决定的，所以我们需要将上面的坐标反推回去。

(−1,−2),(−1,−3),(−1,−4),(−2,−1),(−2,−2),(−2,−3),(−3,−1),(−3,−2),(−4,−1)(-1,-2),(-1,-3),(-1,-4),(-2,-1),(-2,-2),(-2,-3),(-3,-1),(-3,-2),(-4,-1)(−1,−2),(−1,−3),(−1,−4),(−2,−1),(−2,−2),(−2,−3),(−3,−1),(−3,−2),(−4,−1)

  那么我们建立一个扩展的坐标数组

//当前位置只能由前面9个位置到达，所以都填了负号public static int[][] dirs={{0,-1},{0,-2},{0,-3},{-1,0},{-1,-1},{-1,-2},{-2,0},{-2,-1},{-3,0}};

  每搜索到一个节点(x,y)，就判断当前的dp[i][j]和dp[x][y]+a[i]哪个大即可，状态转移方程如下：
dp[i][j]=Math.max(dp[i][j],dp[x][y]+a[i][j])dp[i][j]=Math.max(dp[i][j],dp[x][y]+a[i][j]) dp[i][j]=Math.max(dp[i][j],dp[x][y]+a[i][j])
  完整代码实现：

import java.io.BufferedReader;
import java.io.IOException;
import java.io.InputStreamReader;
import java.io.StreamTokenizer;
import java.util.Arrays;
//dp[i][j]表示从(1,1)到达(i,j)位置获得的最大权值
public class Main {//当前位置只能由前面9个位置到达，所以都填了负号public static int[][] dirs={{0,-1},{0,-2},{0,-3},{-1,0},{-1,-1},{-1,-2},{-2,0},{-2,-1},{-3,0}};public static StreamTokenizer st=new StreamTokenizer(new BufferedReader(new InputStreamReader(System.in)));public static void main(String[] args) throws IOException {int n = nextInt();int m = nextInt();int[][] a = new int[n + 1][m + 1];int[][] dp = new int[n + 1][m + 1];for (int i = 1; i <=n; i++) {for (int j = 1; j <=m ; j++) {a[i][j]=nextInt();}}for (int[] ints : dp) {Arrays.fill(ints,Integer.MIN_VALUE);}dp[1][1]=a[1][1];//初始化for (int i = 1; i <=n ; i++) {for (int j = 1; j <=m; j++) {for (int k = 0; k <9; k++) {//9个位置扩展//扩展int x = i + dirs[k][0];int y = j + dirs[k][1];if(x>=1&&x<=n&&y>=1&&y<=m){ //判断是否越界dp[i][j]=Math.max(dp[i][j],dp[x][y]+a[i][j]);}}}}System.out.println(dp[n][m]);}public static int nextInt() throws IOException {st.nextToken();return (int)st.nval;}
}

2.2 解法二：DFS深度优先搜索最大权值

  使用深度优先遍历，我们对可扩展的方向进行DFS,每次找到终点(n,m)(n,m)(n,m)的时候我们就更新一下最大权值即可。

  但是请注意，现在我们是从左上往右下走，所以坐标是正的，此时扩展的方向数组为：

  //这里是往右下方向走，所以坐标都是正的public static int[][] dirs={{0,1},{0,2},{0,3},{1,0},{1,1},{1,2},{2,0},{2,1},{3,0}};

  完整代码如下：

import java.io.BufferedReader;
import java.io.IOException;
import java.io.InputStreamReader;
import java.io.StreamTokenizer;
public class Main {//这里是往右下方向走，所以坐标都是正的public static int[][] dirs={{0,1},{0,2},{0,3},{1,0},{1,1},{1,2},{2,0},{2,1},{3,0}};public static int n;public static int m;public static int[][] a;public static int cnt=0;public static StreamTokenizer st=new StreamTokenizer(new BufferedReader(new InputStreamReader(System.in)));public static void main(String[] args) throws IOException {n = nextInt();m = nextInt();a = new int[n + 1][m + 1];for (int i = 1; i <=n; i++) {for (int j = 1; j <=m ; j++) {a[i][j]=nextInt();}}dfs(1,1,a[1][1]);System.out.println(cnt);}public static void dfs(int x,int y,int res){if(x==n&&y==m){ //到达终点之后，更新权值和cnt=Math.max(cnt,res);return;}//开始扩展for (int[] dir : dirs) {//(x,y)下一个位置的坐标(ex,ey)int ex = x + dir[0];int ey = y + dir[1];if(ex>=1&&ex<=n&&ey>=1&&ey<=m){ //判断是否越界dfs(ex,ey,res+a[ex][ey]);}}}public static int nextInt() throws IOException {st.nextToken();return (int)st.nval;}
}

  这道题有点类似于那个数字三角形，那个题是只能往右边或者下边走，同样反推回去建立可扩展的坐标数组即可。