leetcode 2348. Number of Zero-Filled Subarrays（0子数组的个数）_股票证券

leetcode 2348. Number of Zero-Filled Subarrays（0子数组的个数）

创始人

2025-06-01 05:52:08

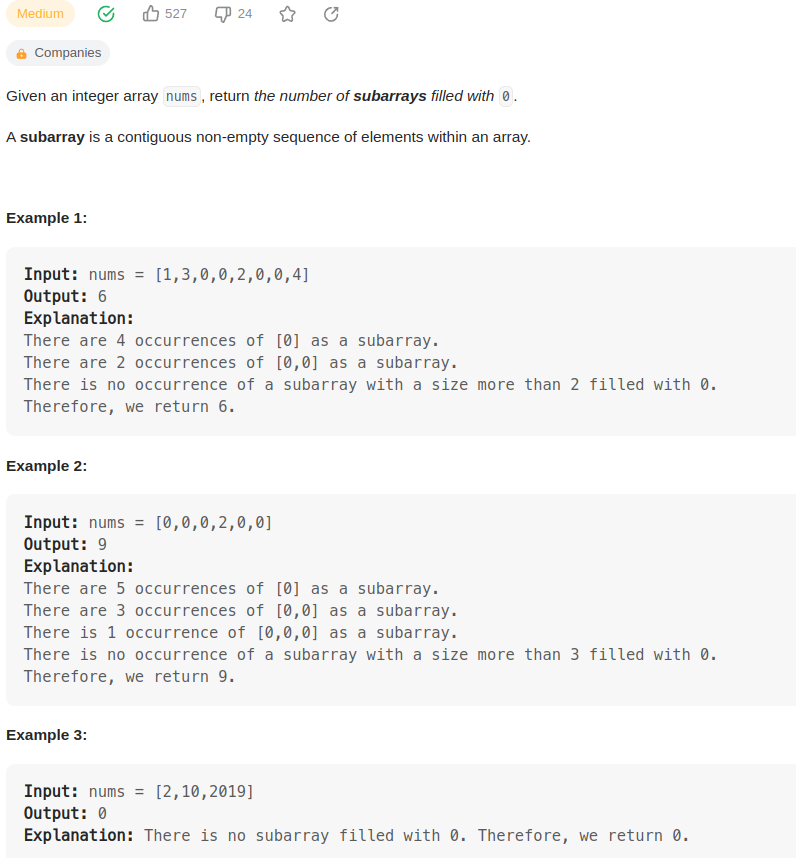
在这里插入图片描述

数组里面数字0组成的连续的子数组一共有多少个。

思路：

数字0的子数组一定全部都是0，不能中间有一个非0数字。

看下规律性：

[0] : 只有一个子数组0.
[0,0]: 注意了2个0是不同的，第1个0和第2个0可以组成2个不同的子数组[0], [0]，
         然后长度为2的两个0又是1个子数组[0,0]。
         所以有1+2 = 3个子数组。
[0,0,0]: 3个0分别是3个长度为1的子数组，还有2个长度为2的，最后是1个长度为3的。
            所以一共有：1+2+3=6个子数组。

同理，如果连续0的个数为n，那么子数组的个数为1+2+…+n.

所以只需要双指针确定0的左边界和右边界，计算出连续0的长度，就可以按上面的方法算出子数组的个数。

把当前下标 i 当作右边界，只要 i 指向非0数字，就计算 i - left 得到连续0 的长度。
每走到1个 i, 就加上当前长度（也可以用(1+n)*n/2计算，但是比这种直接加的慢）。

注意结果要用long类型，因为数量可能会非常多，int会溢出（返回参数也是long).

    public long zeroFilledSubarray(int[] nums) {long res = 0;int left = -1;int n = nums.length;for(int i = 0; i < n; i++) {if(nums[i] != 0) left = i;else res += (i - left);}return res;}

上一篇：实测分享“红豆到底是不是有挂”(的确有挂)

下一篇：玩家实测“新道游牛牛有没有挂吗”分享装挂详细步骤

leetcode 2348. Number of Zero-Filled Subarrays（0子数组的个数）

思路：

相关内容

热门资讯