问题提出：

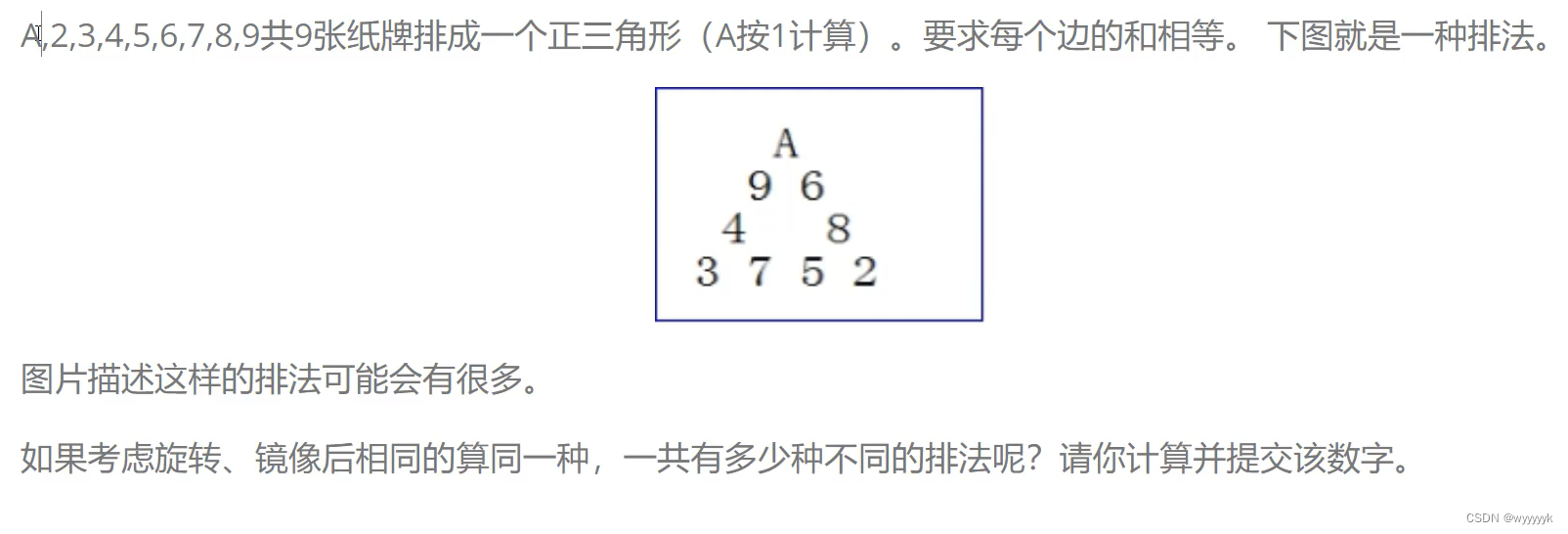
上述问题就是典型的全排列问题！！

一、回溯法

• 回溯：就是类似枚举的搜索尝试过程。在搜索过程中寻找问题的解。当发现不满足求解的条件时，就回溯返回，尝试别的路径。

全排列可以使用试探的方法列举所有的可能性。一个长度为n的序列，所有排列组合：n！

1.从集合中选取一个元素(n种情况)，并标记该元素已被使用
2.在第一步的基础上递归到下一层，从剩余的n-1个元素中，按照第一步的方法找到一个元素，并标记(n-1)
3.以此类推，所有元素都被标记，将元素存起来，去对比求解的情况

在解题前我们先给定数组在三角形上的对应下标：

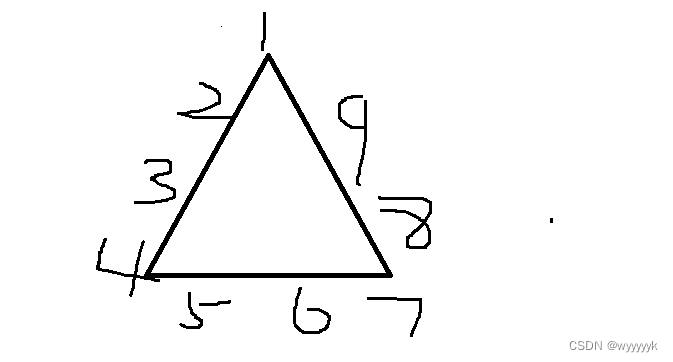
代码实现：

public class 全排列_回溯法 {static int count = 0;// 记录总个数static boolean[] bool = new boolean[10];static int[] arr = new int[10];// 存放数据public static void main(String[] args) {dfs(1);System.out.println(count / 6);//144}public static void dfs(int step) {// 结束条件if (step == 10) {if (arr[1] + arr[2] + arr[3] + arr[4] == arr[4] + arr[5] + arr[6] + arr[7]&& arr[1] + arr[2] + arr[3] + arr[4] == arr[7] + arr[8] + arr[9] + arr[1]) {count++;}return;}for (int i = 1; i < 10; i++) {// 判断i位置上是否放置了数字if (!bool[i]) {arr[step] = i;bool[i] = true;dfs(step + 1);bool[i] = false;}}}
}

二、邻里交换法

• 邻里交换法：

回溯是试探性填充数据，给每个位置都试探性赋值
邻里交换，也是通过递归实现，但是是一种基于交换的思路

步骤：

1.将数组分为2个部分，暂时确定部分和未确定部分，刚开始都是未确定部分在未确定的部分中，让每一个数据都有机会和未确定部分中的第一位交换，然后第一位就变成暂时确定部分。
2.以此类推：每个数据都和未确定部分中的第二位交换（第一位数据除外）...直到确定所有数据。
3.将确定好的数据和条件对比，对比结束后，还原数据。

代码实现：

public class 全排列_邻里交换法 {static int count = 0;static int[] arr = { 1, 2, 3, 4, 5, 6, 7, 8, 9 };public static void main(String[] args) {f(arr, 0);System.out.println(count / 6);//144}public static void f(int arr[], int step) {if (step == arr.length - 1) {if (arr[0] + arr[1] + arr[2] + arr[3] == arr[3] + arr[4] + arr[5] + arr[6]&& arr[0] + arr[1] + arr[2] + arr[3] == arr[6] + arr[7] + arr[8] + arr[0]) {count++;}return;}for (int i = step; i < arr.length; i++) {// 交换{int temp = arr[i];arr[i] = arr[step];arr[step] = temp;}f(arr, step + 1);// 还原数据{int temp = arr[i];arr[i] = arr[step];arr[step] = temp;}}}}

三、暴力解法

public class 全排列_暴力解法 {static int count = 0;public static void main(String[] args) {for (int a = 1; a <= 9; a++) {// 1for (int b = 1; b <= 9; b++) {// 2for (int c = 1; c <= 9; c++) {// 3for (int d = 1; d <= 9; d++) {// 4for (int e = 1; e <= 9; e++) {// 5for (int f = 1; f <= 9; f++) {// 6for (int g = 1; g <= 9; g++) {// 7for (int h = 1; h <= 9; h++) {// 8for (int i = 1; i <= 9; i++) {// 9// 不能重复if (a == b || a == c || a == d || a == e || a == f || a == g || a == h|| a == i || b == c || b == d || b == e || b == f || b == g|| b == h || b == i || c == d || c == e || c == f || c == g|| c == h || c == i || d == e || d == f || d == g || d == h|| d == i || e == f || e == g || e == h || e == i || f == g|| f == h || f == i || g == h || g == i || h == i) {continue;}if (a + b + c + d == d + e + f + g && a + b + c + d == g + h + i + a) {count++;}}}}}}}}}}System.out.println(count / 6);//144}
}